The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
Q4πε0r for points outside and Q4πε0R for points inside the shell
Q4πε0e for both points inside nad outside the shell
zero for points outside and Q4πε0r for points inside the shell
zero for both points inside and outside the shell
The correct Answer is:A
To find the electrostatic potential V of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the center, we need to consider two cases: when the point of interest is inside the shell (i.e., r<R) and when it is outside the shell (i.e., r≥R).
Step 1: Determine the potential inside the shell (when r<R)
For a uniformly charged thin spherical shell, the electric field inside the shell is zero. Therefore, the potential V inside the shell is constant and equal to the potential at the surface of the shell.
The potential at the surface of the shell can be calculated using the formula:
V=KQR
where K=14πϵ0.
Thus, for r<R:
Vinside=KQR
Step 2: Determine the potential outside the shell (when r≥R)
For points outside the shell, the shell can be treated as a point charge located at its center. The potential at a distance r from the center is given by:
V=KQr
Thus, for r≥R:
Voutside=KQr
Conclusion
In summary, the electrostatic potential V of a uniformly charged thin spherical shell is given by:
- For r<R:
V=KQR
- For r≥R:
V=KQr
V=KQR
where K=14πϵ0.
Vinside=KQR
V=KQr
Voutside=KQr
- For r<R:
V=KQR
- For r≥R:
V=KQr
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View Solution
Knowledge Check
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A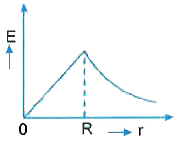 B
B CD
CD
Flux (ph) as a function of distance (r) from centre of uniformly charged solid sphere of charge Q and radius R, is best represented by
A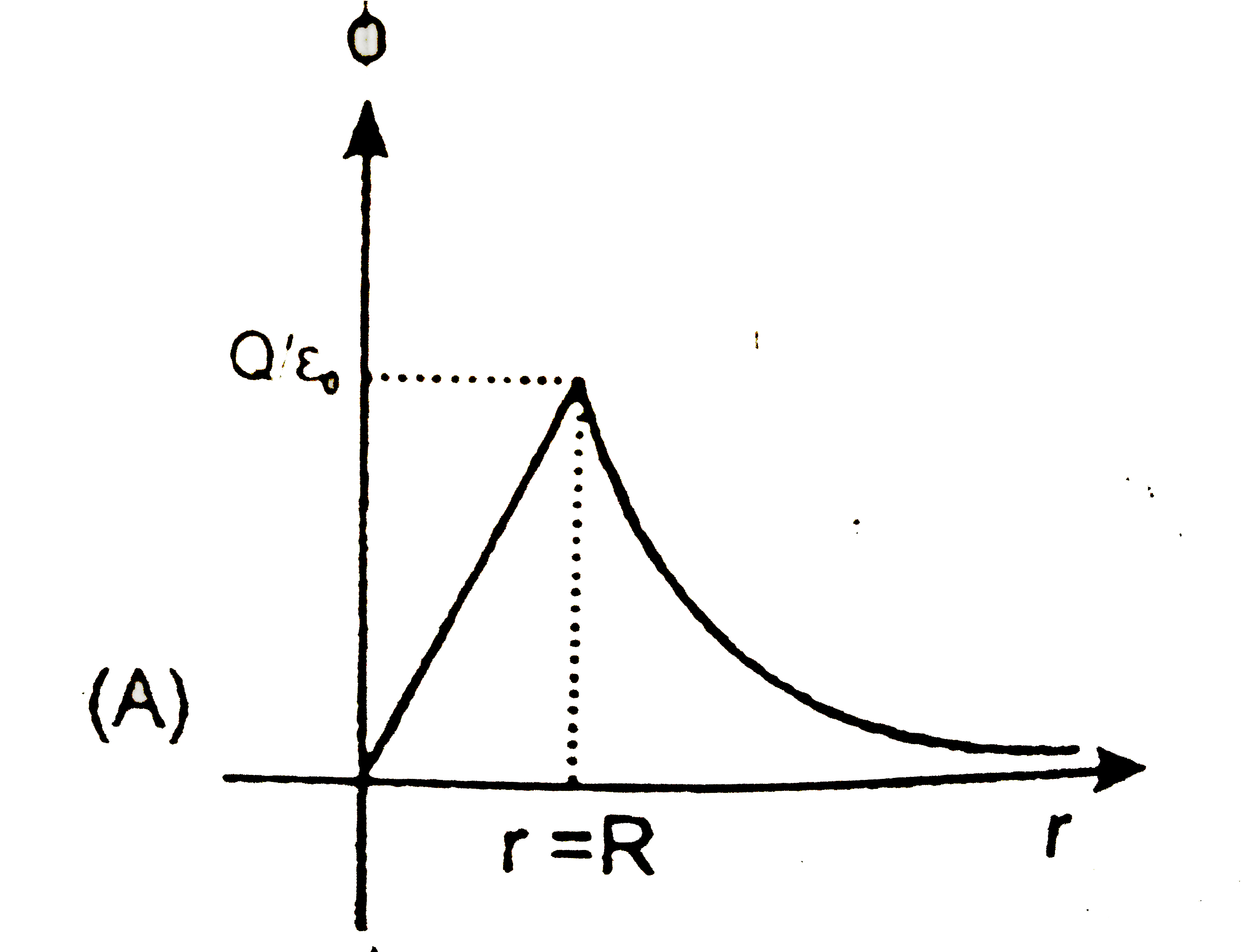 B
B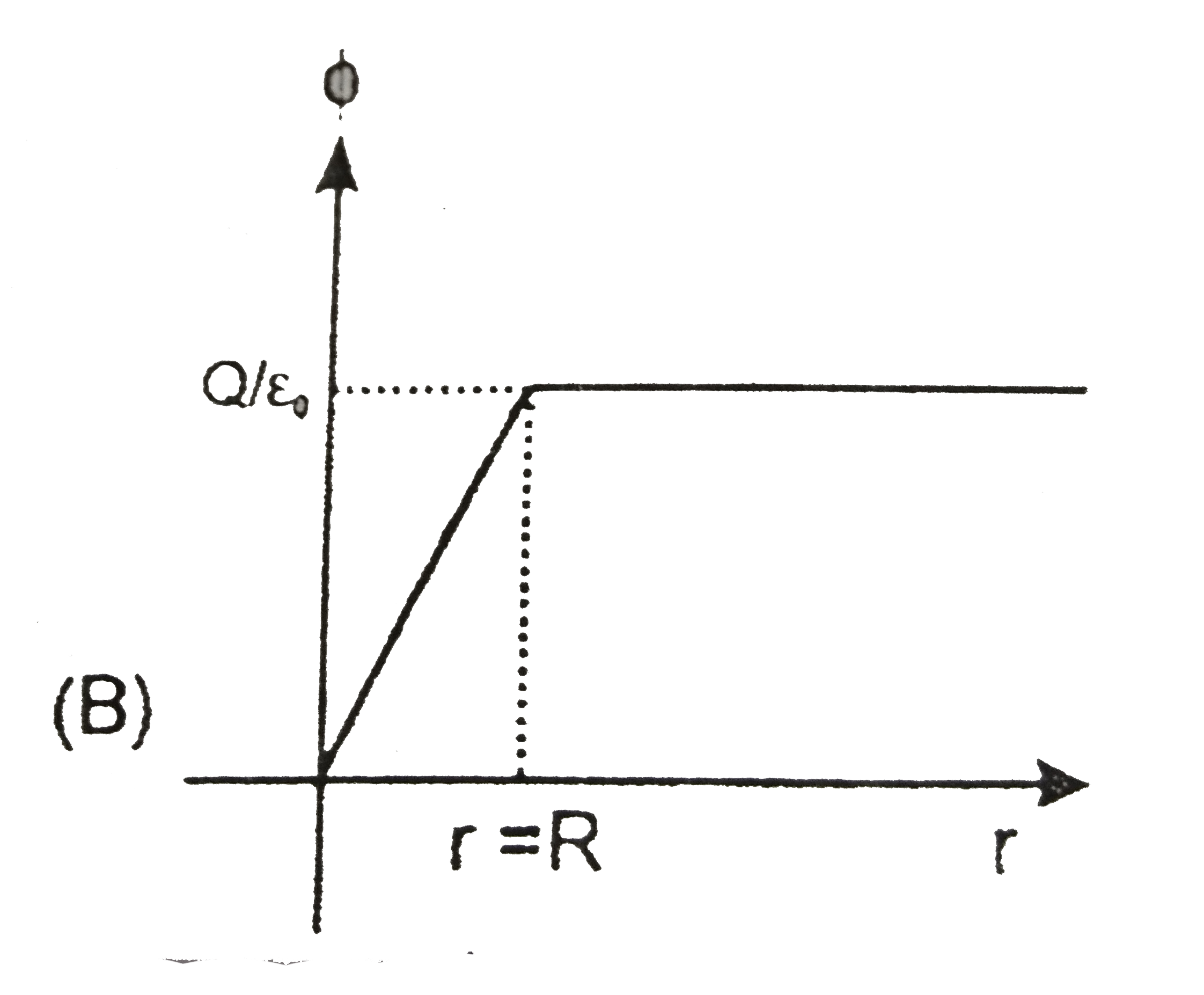 C
C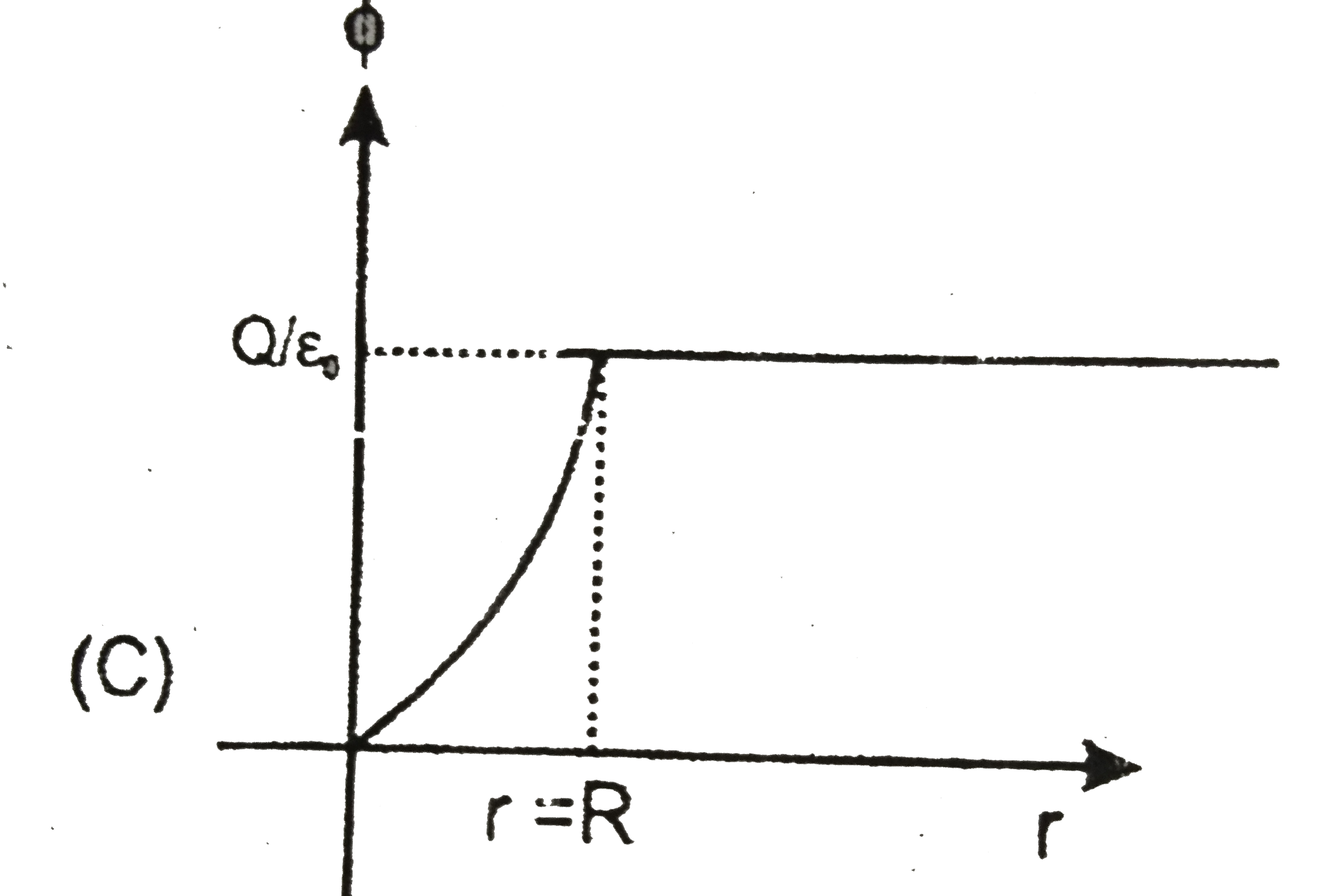 D
D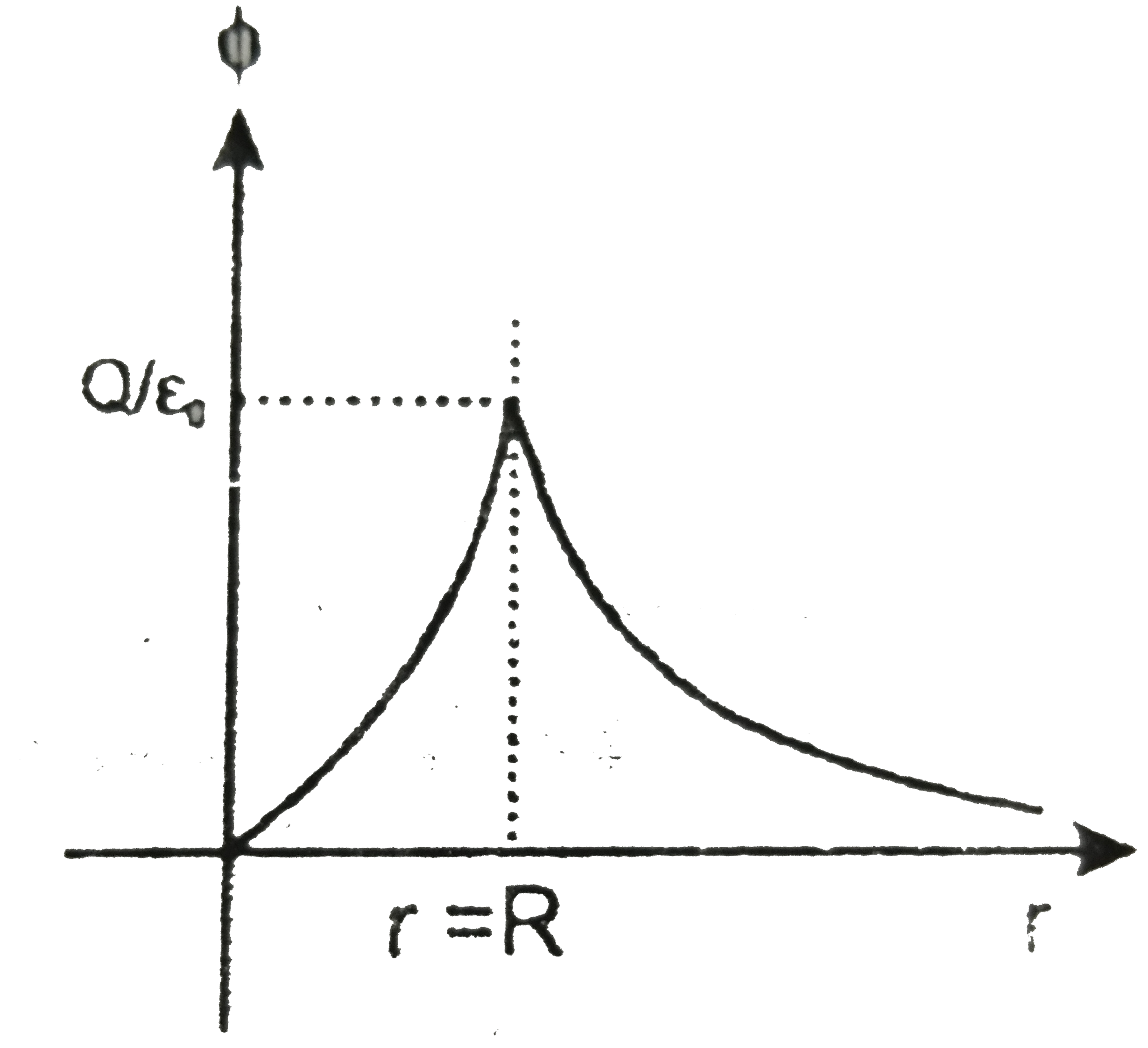
The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
AEB3E2CE2DZero
A point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radiu R is E. The electric field at a distance R2 from the centre of the sphere is:
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R fro the centre of the shell. The electric potential at the centre of shell will (potential at infinity is zero).
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View Solution
