The radii of two concentric spherical conducting shells are r1andr2(>r1). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
q(r2r1)
q2(r1r2)
−q(r1/r2)
q2(r2r1)
The correct Answer is:C
Step by step video, text & image solution for The radii of two concentric spherical conducting shells are r_(1) and r_(2)(gt r_(1)). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.3
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). Find the charge on the inner shell and charge distribution.
View SolutionThere are two concentric metal shells of radii r1 and r2(>r1). If initially, the outer shell has a charge q and the inner shell is having zero charge and then inner shell is grounded. Find :
(i) Charge on the inner surface of outer shell.
(ii) Final charges on each sphere.
(iii) Charge flown through wire in the ground.
View Solution
Knowledge Check
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1There are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
A−QrRB−QRrC−2QRrD−Q)Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A−r2r1qBzeroC−r1r2qD−q
In a system of two concentric spherical conducting shells charge q is given to both inner and outer shells as shown in figure 1.361. Inner shell is connected to earth by a switch Find the amount of heat produced when switch is closed

[5Kq28a]
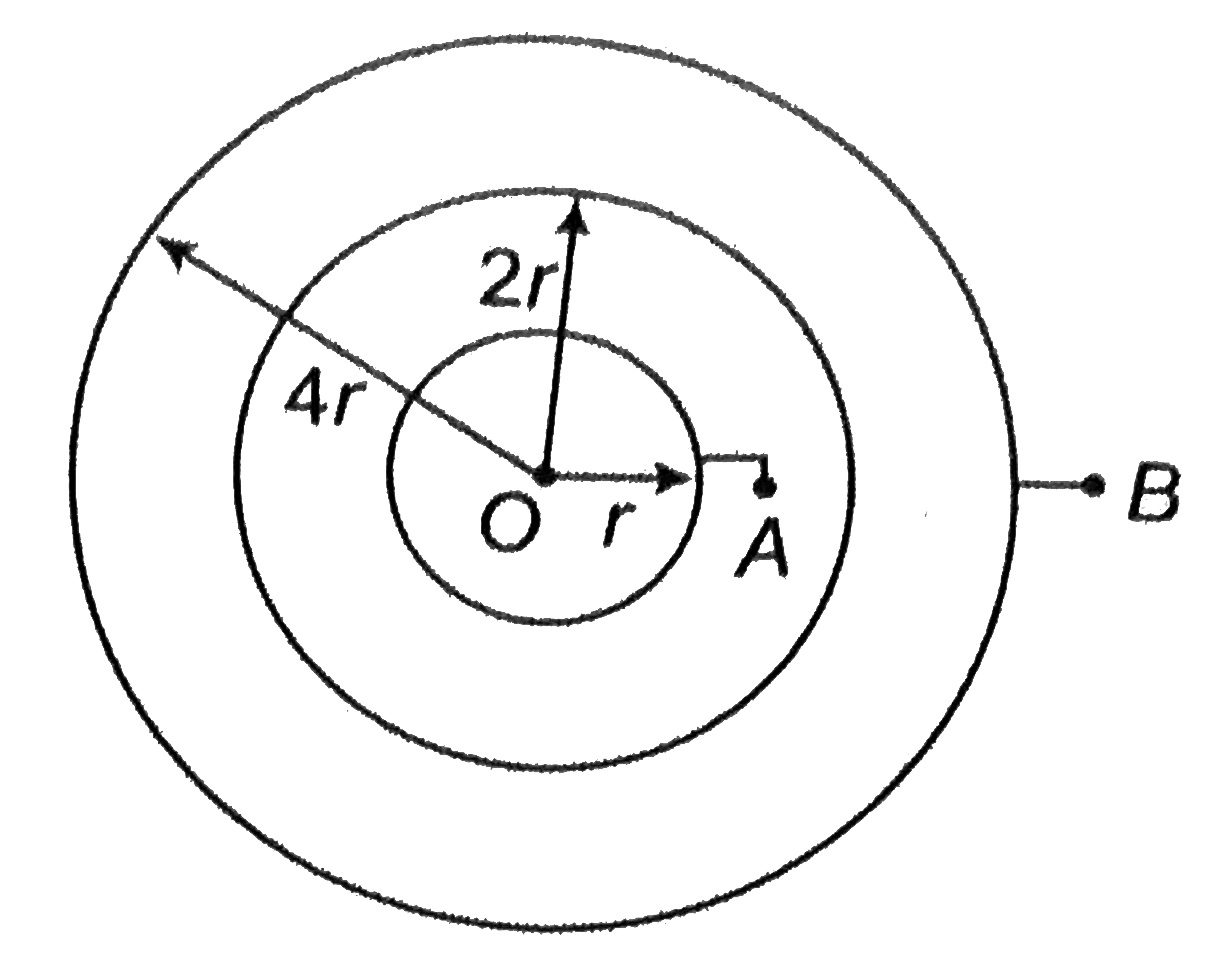
View SolutionFind the equivalent cappacitance between A and B.
(a) Three conducting concentic shells of radii r,2r and
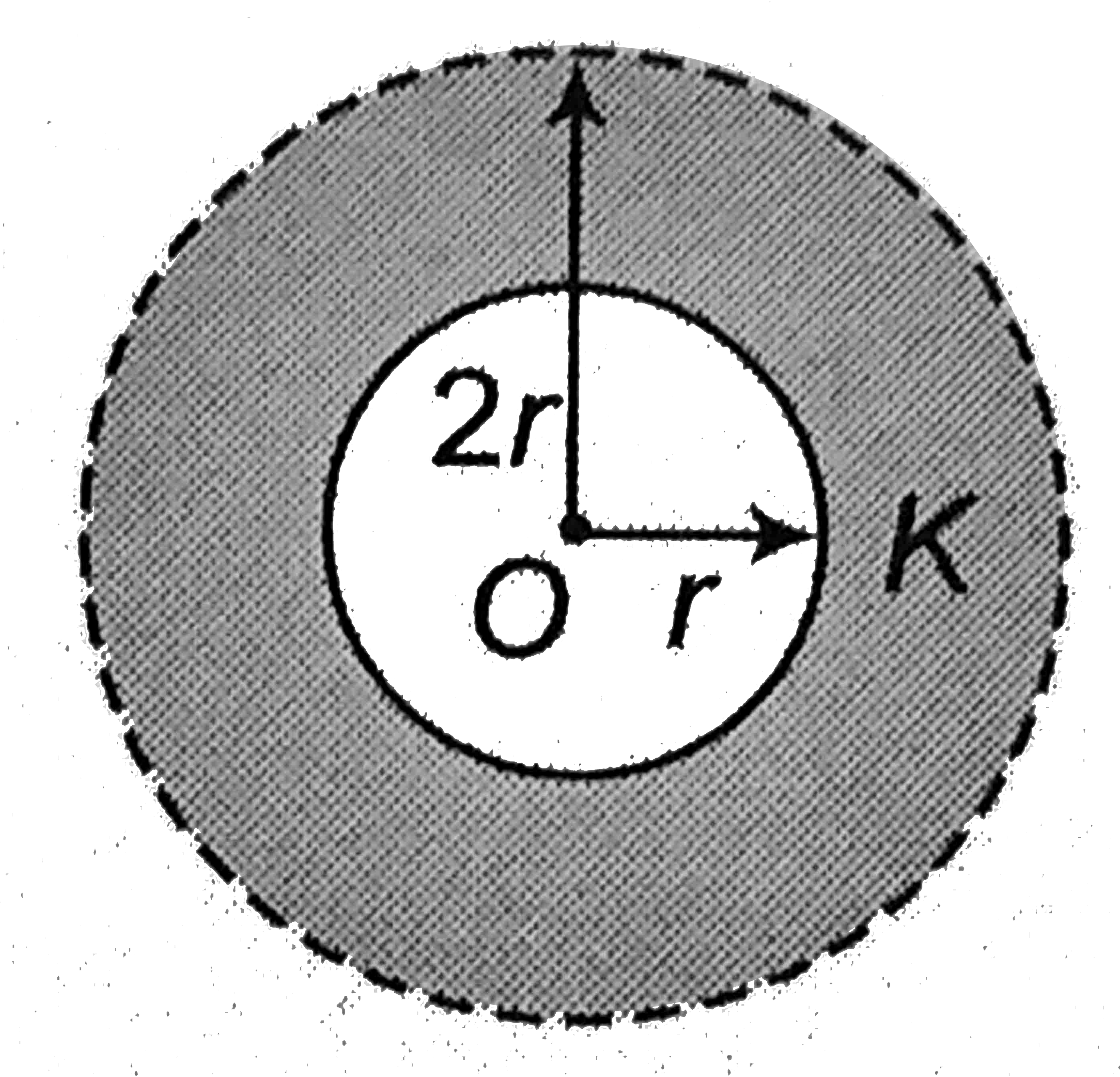
(b) An isoltated ball-shaped conductor of radius r surrounded by an adjuacent layer of dielectric (K) and outer radius 2r.
Two conducting concentic spherical shells having radii r1 and r2(r2>r1), calculate capacity of the system if
(i) The inner shell is given a charge and outer is connected to the earth.
(ii) The outer shell is given a charge and inner is connected to the earth.
(d) Find capacitance of the system
(i) Two shells of radii r1 and r2 having charges are connected by a metallic wire, the separation between shells is large.
(ii) Two shells of radii r1 and r2 carry equal and opposite charges and are separated by a distance d.

View SolutionThere are two concentric conducting spherical shells of radii 10 cm and 20 cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThere are three concentric metallic spherical shells of radius R, 2R and 3R. Charge Q is given to the innermost spherical shell. If the innermost spherical shell is connected with a metal wire to the outermost spherical shell without touching the middle shell, which is connected to the earth, then, find charges appearing on all surfaces.
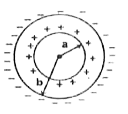
View SolutionThere are two concentric spherical shells with inner shell having positive charge q and outer shell having a charge -q. Now outer shell is supplied a charge -2g and inner shell is earthed, Calculate the ratio of initial and final capacities of the system. (If a = 3R, b= 5 R)
View Solution
