Two hypothetical planets $1$ and $2$ are moving in the same eliptical path as shown in the figure. If the planets are situated at minimum and maximum distance from the sun and one of the planet, say $1$ , has speed $v$ . Find the relative angular speed of the planets for the given situation.

Video Solution

Text Solution

Verified by Experts

According to Kelper.s Law of area $(1 / 2) r^{2} ω =$ constant.
$\Rightarrow r_{1}^{2} ω_{1} = r_{2}^{2} ω_{2}$
$\Rightarrow \frac{ω_{2}}{ω_{1}} = {(\frac{r_{1}}{r_{2}})}^{2}$
$\Rightarrow \frac{ω_{2}}{ω_{1}} = {(\frac{r}{2 r})}^{2} \Rightarrow ω_{2} = \frac{ω_{1}}{4}$ ,
Putting $ω_{1} = \frac{V_{1}}{r_{1}} = \frac{V}{r}$ ,
We obtain , $ω_{2} = \frac{V}{4 r}$ .
Since the direction of angular velocities $ω_{1}$ and $ω_{2}$ are same, the relative angular speed
$ω_{r} = | ω_{1} - ω_{2} | = ∣ ∣ ∣ (\frac{V}{r} - \frac{V}{4 r}) ∣ ∣ ∣ \Rightarrow ω_{r} = \frac{3 v}{4 r}$ .

Updated on:21/07/2023

A planet of mass $m$ moves along an ellipse around the sun so that its maximum and minimum distance from the sun are equal to $r_{1}$ and $r_{2}$ respectively. Find the angular momentum of this planet relative to the centre of the sun. mass of the sun is $M$ .
A $m \sqrt{\frac{2 G M r_{1} r_{2}}{{(r_{1} + r_{2})}_{1}^{2}}}$
B $m \sqrt{\frac{2 G M r_{1}^{2} r_{2}^{2}}{{(r_{1} + r_{2})}_{1}^{2}}}$
C $m \sqrt{\frac{2 G M r_{1}^{2} r_{2}^{2}}{(r_{1} + r_{2})}}$
D $m \sqrt{\frac{2 G M r_{1} r_{2}}{(r_{1} + r_{2})}}$
A planet is revolving in an elliptical orbit about the sun. Its closest distance is R. If $K_{1} and K_{2}$ are the maximum and minimum kinetic energies of the planet, $K_{1} / K_{2}$ =
A $R / r$
B $\sqrt{R / r}$
C $R^{2} / r^{2}$
D1
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

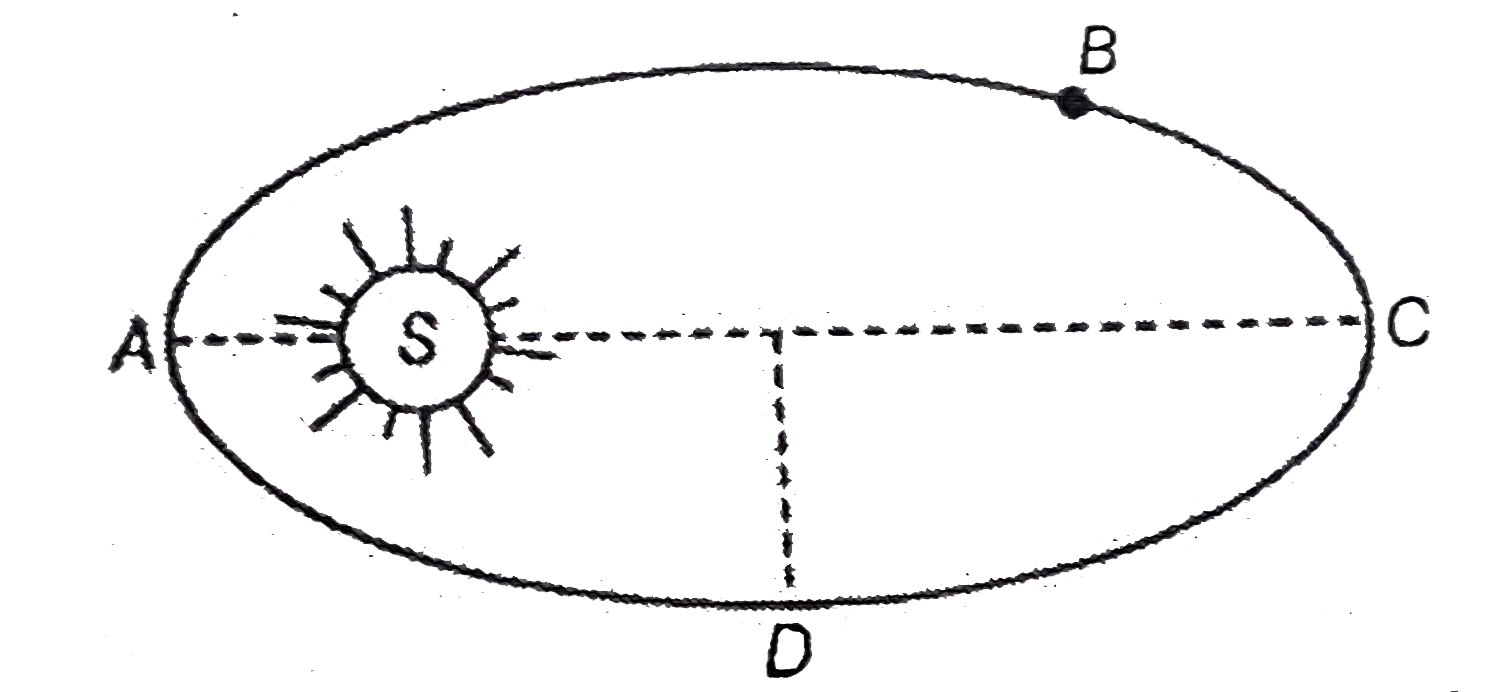AA
BB
CC
DD