A uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
The gravitational field at a distance of 1.5r from the centre is 29Gmr2
The gravitational field at a distance of 2.5r from centre is 825Gmr2
The gravitational field at a distance of 1.5r from centre is zero
The gravitational field between the sphere and spherical shell is uniform.
The correct Answer is:B
At distance 2.5 r or 52r

E=G(m+m)(52r)2=8Gm25r2.
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.4
Explore 10 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.5
Explore 20 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.2
Explore 20 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
A uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherica shel of equla mass and radius 2a.Find the gravitational field at a distance a. 3/2 a from the centre , b. 5/2 as from the centre.
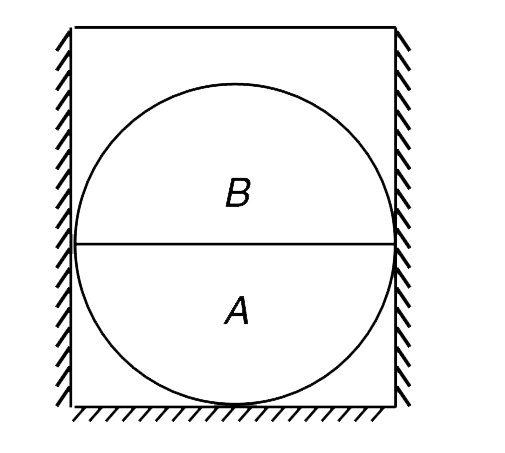
View SolutionA uniform solid hemisphere A of mass M radius R is joined with a thin uniform hemispherical shell B of mass M and radius R (see fig.). The sphere thus formed is placed inside a fixed box as shown. The floor , as well as walls of the box are smooth. On slight disturbance, the sphere begins to rotate. Find its maximum angular speed (ω) and maximum angular acceleration (α0) during the subsequent motion. Do the walls of the box apply any force on the sphere while it rotates ?
View Solution
Knowledge Check
A uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is
 AGMmx2BGMmxR3CG(M=m)x2DZero
AGMmx2BGMmxR3CG(M=m)x2DZeroA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√rgB2pi sqrt((5 R)/(3 g))C2π√7R5gD2π√2R5gThe M.I. of solid sphere of mass M and radius R about its diameter is
A25MR2B75MR2C23MR2D53MR2
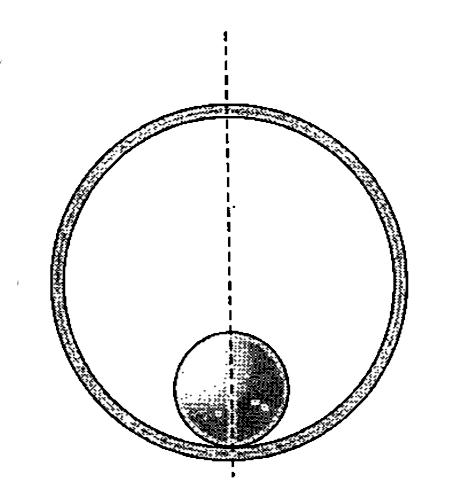
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View SolutionFor a uniform ring of mass M and radius R at its centre
View Solution_E01_069_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QIn what time will it enter the hole at A
View Solution

