An arrangedment illlustrated in figure consists of a horizontal uniform disc D of mass m and radius R and a thin rod AO whose torsional coefficient is equal to k. Find the amplitude and the energy of small torsional oscillationa if at the initial momentu the disc was deviated through an angle φ0 from the equilibrium position and then imparted an angular velocity φ0.
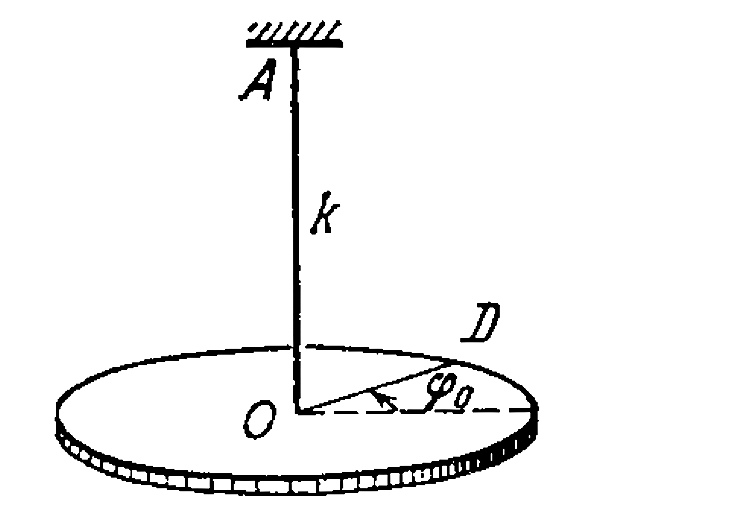
The K.E. of the disc is 12I.φ2=12(mR22).φ2=14mR2.φ2
The torsional potential energy is 12kφ2. Thus the total energy is :
14mR2.φ2+12kφ2=14mR2..φ20+12kφ20
By definition of the amplitude φm,.φ=0 when φ=φm . Thus total energy is
12kφ2m=14mR2.φ20+12kφ20
orφm=φ0
⎷1+mR22kφ20φ20
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A uniform rod of mass m and length l performs small oscillations about the horizontal axis passing throughits upper end. Final the mean kinetic energy of the rod averaged over one oscillation period it at the initial mment it was deflected from the vertical by an angle θ0 and then imparted an angular velocity θ0.
View SolutionFind the elastic deformation energy of a steel rod whose one end is fixed and the other is twisted through an angle φ=6.0∘. The length of the rod is equal to l=1.0m, and the radius to r=10mm.
View Solution
Knowledge Check
A uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
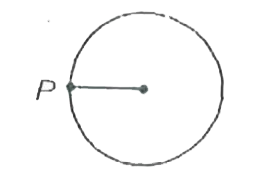 A2gcosθ3RBgsinθ2RC2gsinθRD2gsinθ3R
A2gcosθ3RBgsinθ2RC2gsinθRD2gsinθ3RA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)
A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
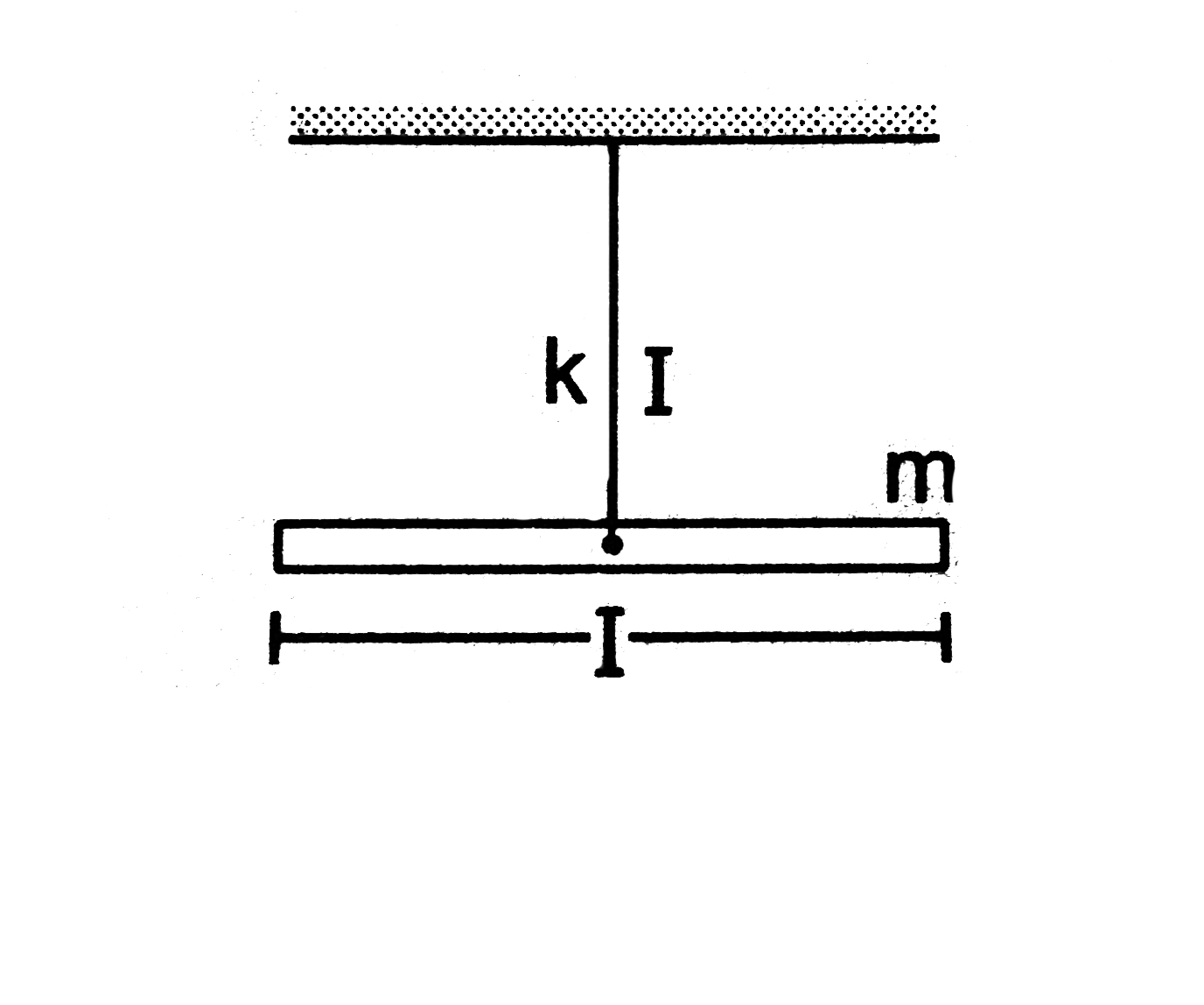
View SolutionFind the period of small torsional oscillational of a system consisting of two discs slipped oon a thin rod with rod with torsional coefficient k. The moments of inertia of discs relative to the rod's axis are equal to I1 and I2.
View SolutionA man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre. At a certain moment the man starts moving along the edge of the disc, he shifts over an angle φ′ relative to the disc and then stops. In the process of motion the velocity of the man varies with time as v′(t).
Assuming the dimensions of the man to be negligible, find:
(a) the angle through which the disc had turned by the moment the man stopped,
(b) the force moment (relative to the rotation axis) with which the man acted on the disc in the process of motion.
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View Solution