A uniform rod of mass m and length l performs small oscillations about the horizontal axis passing throughits upper end. Final the mean kinetic energy of the rod averaged over one oscillation period it at the initial mment it was deflected from the vertical by an angle θ0 and then imparted an angular velocity θ0.
Moment of inertia of the rod equals ml23 about its one end and perpendicular to its length. Thus rotational kinetic of the rod =12(ml23).θ2=ml26.θ2
when the rod is displaced by an angle θ its C.G. goes up by a distance l2(1−cosθ)≅lθ24 for small θ
Thus the P.E. becomes :mg(lθ24)
As the mechanial energy of oscillation fo the rod is conserved .
12(ml23).θ2+12(mgl2)θ2= Constant
on differenticating w.r.t. time and for the simplifies we get :..θ=−3g2lθ for small θ.
we see tha the angular frequency ω is
=√3g/2l
we write the general solution of the angular oscillation is :
θ=Acosωt+Bsinωt
But θ=θ0 at t=0, so A=θ0
and θ=θ0 at t=0, so
B=θ0/ω
Thus θ=θ0cosωt+θ0ωsinωt
Thus the K.E. of the rod
T=ml26.θ2=[−ωθ0sinωt+.00cosωt]2
=ml26[.θ20cos2ωt+ω2θ20sin2ωt−2ω00.00sinωtcosωt]
On averaging over one time period the last term vanishes and <sin2ωt>=<cos2ωt<=1/2. Thus
<T>=112ml2.θ20+18mgl2θ20 ( where ω2=3g/2l)
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A uniform rod of length l performs small oscillations about the horizontal axis OO′ perpendicular to the rod and passing through one of its points. Find the distance the centre of inertia of the rod and the axis OO′ at which the oscillation period is the shortest. What is it equal to ?
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
Aml23Bml23sinθCml23sin2θDml23cos2θ
A uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
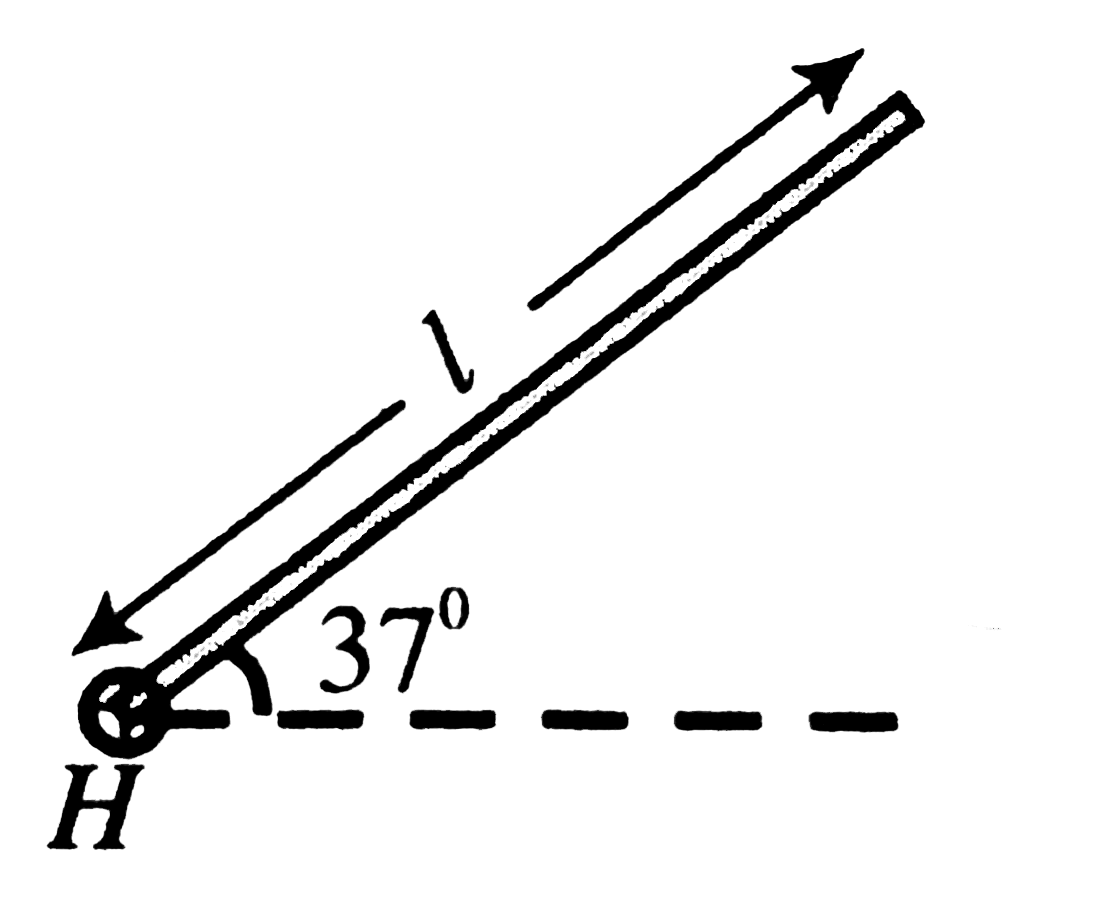
View SolutionA uniform. rod of length l can rotate without friction about an axis passing through its upper end (Fig). The rod is deflected by an angle a0 and let go. Find the speed of the lower end of the rod as a function of the angle α
View SolutionA uniform rod of mass m and length / makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View Solution

