A plane electromagnetic wave falls at right angles to the surface of a plane − parallel plate of thickness l . The plate is made of non− magentic substance whose permittivity decreases exponentially from a value ε10 at the front surface down to a value ε2 at the rear one. How lond does it take a given wave phase to travel across this plate gt
From the data of the problem the relative permittivity of the medium varies as
ε(x)=ε1e−(x/l)1nε1ε2
Hence the local velocity of light
v(x)=c√ε(x)=c√ε1ex2l1nε1ε2
Thus the required time t=∫l0dxv(x)=√ε1c∫l0e−x2l1nε1ε2
dx=√ε1c=e−121nε1ε2+112l1nε1ε2=2lc√ε1−√ε21nε1ε2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A beam of monichromatic light falls normally on the surfcae of a plane-parallel plate of thickness l. The absorption coefficient of the substance the plate is made of varies linearly along the normal to its surfcae from x1 to x2. The coefficient of reflection at each surface of the plate is equal to ρ. Neglecting the secondary reflections, find the transmission coefficient of such a plate.
View SolutionA parallel plate capacitor with plates of length l is included in a circuit as shown in figure-3.164. The EMF of the source is ε, its internal resistance is r and the distance between the plates is d. An electron with a velocity u files into the capacitor, parallel to the plates . What resistance R should be connected in parallel with the capacitor so that the electron files out of the capacitor at an angle of 37∘ to the plates? Assume that circuit is in steady state. Given values of parameters as l=91cmε=3V,r=2Ω,d=(1/3)mm,u=4×107m/sme=9.1×10−31kg and e=1.6×10−19C.
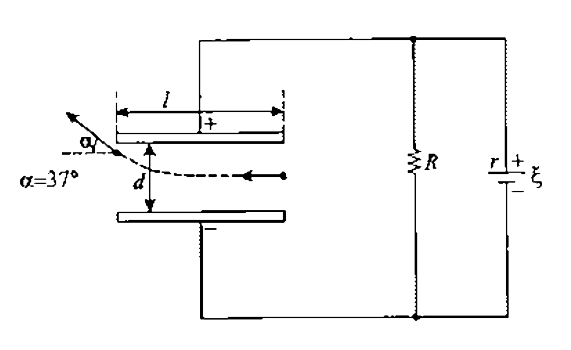
View Solution
Knowledge Check
This question has a paragraph followed by two statements, Statement - 1 and Statement - 2. Of the given four alternatives after the statements, choose the one that describes the statements. A thin air film is formed by putting the convex surface of a plane-convex lens over a plane glass plate. With monochromatic light, this film gives an interference pattern due to light reflected from the top (convex) surface and the bottom (glass plate) surface of the film.
Statement - 1: When light reflects from the air-glass plate interface, the reflected wave suffers a phase change of π.
Statement - 2 : The centre of the interference pattern is dark.AStatement - 1 is true, Statement - 2 is true, Statement - 2 is the correct explanation of Statement -1.BStatement - 1 is true, Statement - 2 is true, Statement - 2 is not the correct explanation of Statement -1.CStatement - 1 is false, Statement -2 is true.DStatement -1 is true, Statement -2 is false.
An infinite plane of uniform dielectric with permittivity ε is uniformly charged with extraneous chagre fo space density ρ. The thickness of the plate is equal to 2d. Find:
(a) the magnitude of the electric field strength and the potential as functions of distance l from the middle point of the plane.(where the potential is assumed to be equal to zero), having chosen teh x coriditnate axis perpendicular to the plate, draw the approximate plots of teh projection Ex(x) of the vector E and the potentail φ(x), plots fo the projection Ex(x) of the vector E adn the potential φ(x),
(b) the surface and space denstites of the bound charge.
View SolutionA beam of light of intensity I0 falls normally on a transparent plane-parallel plate of thickness l. The beam contains all the wavelengths in the interval from λ1 to λ2 of equal spectral intensity. Find the intensity of the transmitted beam if in this wavelength interval the absorption coefficient is a linear function of λ, with exterme values x1 and x2. The coefficient of reflection at each surfcae is equal to ρ. The secondary reflections are to be neglected.
View SolutionMagnetic flux ϕB through a plane of area 'A' placed in a uniform magnetic field vceB is given as:
ϕB=vceB.vceA=BAcosθ
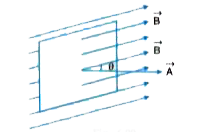
where θ is the angle between vceB and vceA. The above relatio can be extended to curved surfaces and non-uniform fields. In general, if the magnetic field has different magnitudes an directions at various parts of a surface, then the magnetic flux through the surface is given by
ϕB=∫→B.d→A
On the basis of the experimental observations, Faraday concluded that an emf is induced in a coil when magnetic flux through the coil changes with time. Faraday stated his conclusions in the form of a law called Faraday's law of electromagnetic induction. As per this law, the induced emf is given by
ɛ=−dϕBdt
The negative sign in the expression indicates the direction of induced emfe and hence the direction of current in a closed loop.
In the case of a closely would coil of N turns, change of flux associated with each turns is the same and so that total induced emf is given by ɛ=−NdϕBdt
From above relations it is clear that the magnetic flux can be changed by changing any one or more of the terms vceB,vceAandθ.
(a) Give SI unit of magnetic flux.
(b) How is it related to tesla ?
(c) Obtain dimensional formula of magnetic flux.
(d) A loop of area 4×10−3m2 is placed with its plane perpendicular to a uniform magnetic field of 0.02 T. If the loop is quickly removed from the magnetic field within a time of 2 ms, what is the magnitude of induced emf across the two ends of the loop ?
(e) If the resistance of the loop be 0.2Ω and a sensitive milliammeter be connected between the two ends of loop, what will be the reading of milliammeter?
View SolutionA plane monochromatic light wave of intensity I0falls normally on a plane-parallel plate both of whose surfaces have a reflection coeffiecient ρ. Taking into account multiple reflections, find the intensity of the transmitted light if
(a) the plate is perfectly transparent, i.e the absorption is absent,
(b) teh coefficient of linear absorption is equal to x, and the plate thickness is d.
View SolutionA dielectric slab is introduced inside an uncharged capacitor of plate area A and plate separation L. The surface area of the slab is A and its thickness is slightly less than L. Let the surfaces of the slab that are facing the plates of the capacitor be called its two “faces”. The dielectric constant of the slab varies with distance x from one of its faces as: K=K0(1+XL), where K0 is a constant. After the insertion of the slab, the capacitance of the capacitor is n(K0ε0ALloge2). The value of n is _________.
View SolutionA metal plate is placed 5m from a monchromatic ligth
soure whose power output is 10−3W. Consider that a given ejected
photoelectron may collect its energy from a circular area of the plate as large as
ten atomic diameters 10−9 m in radius. The energy required to remove an electron through the metal surface is about 5.0 eV. Assuming light to be a
wave, how long would it take for such a 'target' to soak up this much energy
from such a light source.
View Solution(a) What is a wave front? How does it propagate? Using Huygens' principle, explain reflection of a plane wavefront from a surface and verify the laws of reflection. (b) A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is obtained on a screen 1 m away. If the first minimum is formed at a distance of 2.5 mm from the centre of screen, find the (i) width of the slit, and (ii) distance of first secondary maximum from the centre of the screen.
View Solution