A dielectric slab is introduced inside an uncharged capacitor of plate area A and plate separation L. The surface area of the slab is A and its thickness is slightly less than L. Let the surfaces of the slab that are facing the plates of the capacitor be called its two “faces”. The dielectric constant of the slab varies with distance x from one of its faces as: K=K0(1+XL), where K0 is a constant. After the insertion of the slab, the capacitance of the capacitor is n(K0ε0ALloge2). The value of n is _________.
The correct Answer is:1
To solve the problem, we need to find the value of n in the expression for the capacitance of a capacitor with a dielectric slab inserted. The dielectric constant K varies with distance x from one of the faces of the slab as given by:
K=K0(1+xL)
1. Understanding the Capacitor Configuration:
- We have a parallel plate capacitor with plate area A and separation L.
- A dielectric slab of thickness slightly less than L is inserted between the plates.
2. Capacitance of a Differential Element:
- Consider a small element of thickness dx at a distance x from one face of the slab.
- The dielectric constant at this position is:
K(x)=K0(1+xL)
- The capacitance dC of this small element can be expressed as:
dC=A⋅K(x)⋅ϵ0dx
3. Substituting for K(x):
- Substitute K(x) into the expression for dC:
dC=A⋅K0(1+xL)⋅ϵ0dx
4. Finding the Total Capacitance:
- Since the dielectric slab is uniform and the capacitors formed by each differential element are in series, we need to find the equivalent capacitance Ceq:
1Ceq=∫L01dC
- Substitute dC into the integral:
1Ceq=∫L0dxA⋅K0(1+xL)⋅ϵ0dx=∫L0dxA⋅K0⋅ϵ0dx+A⋅K0⋅xL⋅ϵ0
5. Evaluating the Integral:
- The integral simplifies to:
1Ceq=1A⋅K0⋅ϵ0∫L0dx1+xL
- The integral can be evaluated:
∫L0dx1+xL=Lln(2)
6. Finding Ceq:
- Thus, we have:
Ceq=A⋅K0⋅ϵ0⋅LLln(2)=A⋅K0⋅ϵ0ln(2)
7. Comparing with Given Expression:
- The problem states that the capacitance is given by:
C=n(K0ϵ0ALln(2))
- By comparing both expressions:
n=1
Final Answer:
The value of n is 1.
- We have a parallel plate capacitor with plate area A and separation L.
- A dielectric slab of thickness slightly less than L is inserted between the plates.
- Consider a small element of thickness dx at a distance x from one face of the slab.
- The dielectric constant at this position is:
K(x)=K0(1+xL)
- The capacitance dC of this small element can be expressed as:
dC=A⋅K(x)⋅ϵ0dx
- Substitute K(x) into the expression for dC:
dC=A⋅K0(1+xL)⋅ϵ0dx
- Since the dielectric slab is uniform and the capacitors formed by each differential element are in series, we need to find the equivalent capacitance Ceq:
1Ceq=∫L01dC
- Substitute dC into the integral:
1Ceq=∫L0dxA⋅K0(1+xL)⋅ϵ0dx=∫L0dxA⋅K0⋅ϵ0dx+A⋅K0⋅xL⋅ϵ0
- The integral simplifies to:
1Ceq=1A⋅K0⋅ϵ0∫L0dx1+xL
- The integral can be evaluated:
∫L0dx1+xL=Lln(2)
- Thus, we have:
Ceq=A⋅K0⋅ϵ0⋅LLln(2)=A⋅K0⋅ϵ0ln(2)
- The problem states that the capacitance is given by:
C=n(K0ϵ0ALln(2))
- By comparing both expressions:
n=1
The value of n is 1.
Similar Questions
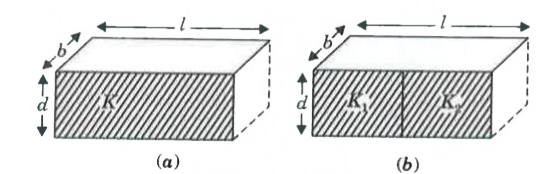
Two identical capacitors of plate dimensions: l×b and plate separation d have dielectric slabs filled in between the space of the plates as shown in the figures. if capacitance of both capacitor is same, Obtain the relation between the dielectric constant K,K1andK2.
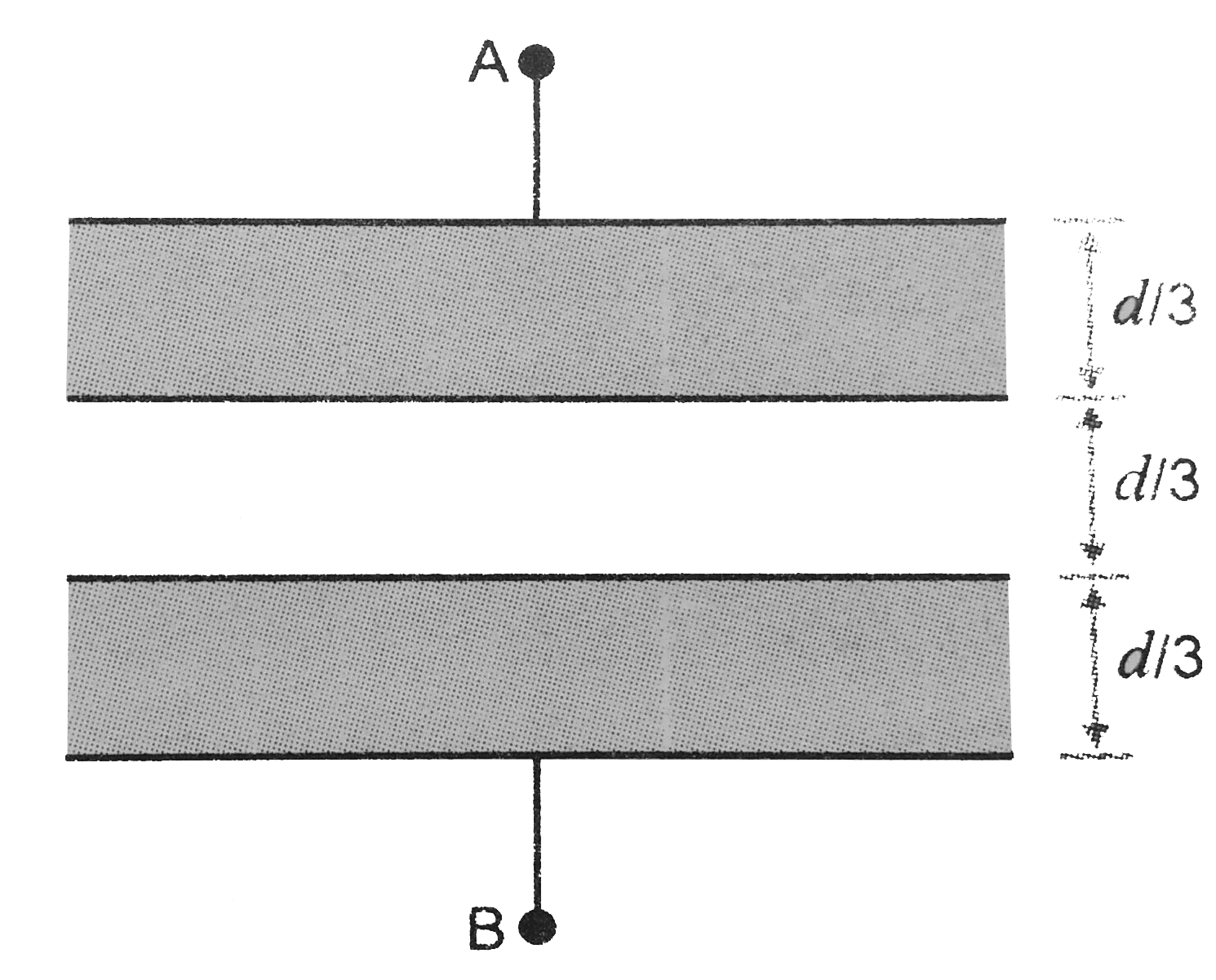
View SolutionFig shows a parallel plate capacitor of plate area A and plate separation d. Its entire space is filled with three different dielectric slabs of same thickness. Find the equivalent capacitance of the arrangment.
View Solution
Knowledge Check
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreasesFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dielectric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab isAVKdBKVdCVdDKVtCapacitance of a capacitor becomes 76 times of its original value if a dielectric slab of thickess t=24d is introduced in between the plates, d is the separation between the plates. The dielectric constant of the dielectric slab is
A1411B1114C711D117
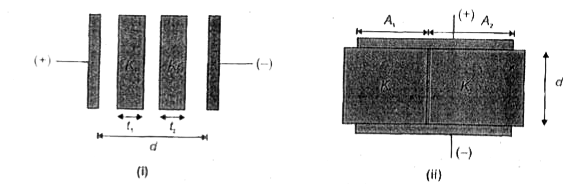
An air-cored capacitor of plate area A and separation d has a capacity C . Two dielectric slabs are inserted between its plates in two different manners as shown . Calculate the capacitance in each case .
View SolutionThe capacitor shown has square plates of side "L" and has gap d between the plates.If the dielectric constant of the material of the slab is "k" ,the capacitance of the capacitor is
View SolutionA parallel - plate capacitor of plate area Aand plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionThe plates of parallel plate capacitor are charged upto 100V. A 2mm thick dielectric slab is inserted between the plates.Then to maintain the same potential difference,the distance between the plates is increased by 1.6mm. The dielectric constant of the slab is.
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates
View Solution

