A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
becomes zero
remains the same
decreases
increases
The correct Answer is:D
To solve the problem regarding the capacitance of a parallel plate capacitor with a dielectric slab inserted, we can follow these steps:
1. Understand the Basic Formula for Capacitance:
The capacitance C of a parallel plate capacitor without any dielectric is given by the formula:
C=ϵ0Ad
where:
- ϵ0 is the permittivity of free space,
- A is the area of one of the plates,
- d is the separation between the plates.
2. Introduce the Dielectric Constant:
When a dielectric material is introduced between the plates, the capacitance increases. The new capacitance C′ can be expressed as:
C′=K⋅C
where K is the dielectric constant of the material.
3. Substitute the Original Capacitance:
Substitute the expression for C into the equation for C′:
C′=K⋅ϵ0Ad
4. Final Expression for Capacitance with Dielectric:
Thus, the capacitance of the capacitor with the dielectric slab becomes:
C′=Kϵ0Ad
5. Conclusion:
The presence of the dielectric slab increases the capacitance by a factor of K. Therefore, the capacitance of the parallel plate capacitor with the dielectric slab is greater than the capacitance without it.
The capacitance C of a parallel plate capacitor without any dielectric is given by the formula:
C=ϵ0Ad
where:
- ϵ0 is the permittivity of free space,
- A is the area of one of the plates,
- d is the separation between the plates.
When a dielectric material is introduced between the plates, the capacitance increases. The new capacitance C′ can be expressed as:
C′=K⋅C
where K is the dielectric constant of the material.
Substitute the expression for C into the equation for C′:
C′=K⋅ϵ0Ad
Thus, the capacitance of the capacitor with the dielectric slab becomes:
C′=Kϵ0Ad
The presence of the dielectric slab increases the capacitance by a factor of K. Therefore, the capacitance of the parallel plate capacitor with the dielectric slab is greater than the capacitance without it.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Fill in the Blanks)
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Short Answer Questions)
Explore 38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Very Short Answer Questions)
Explore 56 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
A dielectric slab of thickness 1.0 cm and dielectric constant 5 is placed between the plates of a parallel plate capacitor of plate area 0.01m2 and separation 2.0 cm. Calculate the change in capacity on introduction of dielectric. What would be on the change, if the dielectric slab were conducting?
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure will be
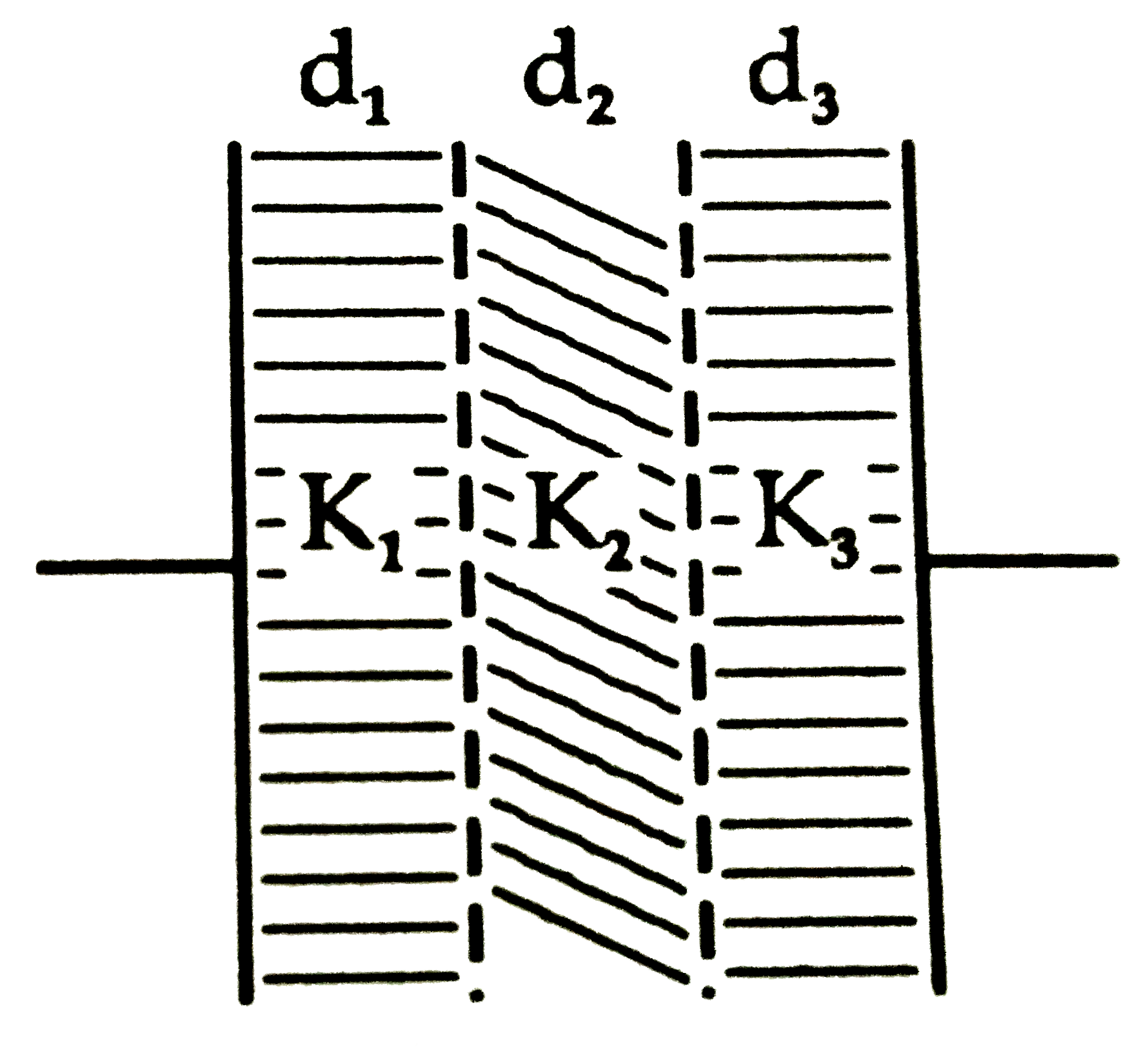
View Solution
Knowledge Check
If a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
ACB2CC3CD4CThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3)A dielectric of thickness 5cm and dielectric constant 10 is introduced between the plates of a parallel plate capacitor having plate area 500 sq. cm and separation between the plates 10cm. The capacitance of the capacitor with dielectric slab is
(ε0=8.8×10−12C2/N−m2)A4.4pFB6.2pFC8pFD10pF
A dielectric slab of thickness 't' is kept between the plates of a parallel plate capacitor separated by a distance 'd' (t<d) . Derive the expression for the capacity of the capacitor .
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View SolutionAs shown in Fig, a dielectric material of dielectric constant K is inserted in half portion between plates of parallel plate capacitor. If its initial capacitance is C, what is the new capacitance ?

View SolutionIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
View SolutionIn the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
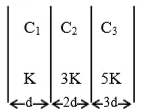
View Solution