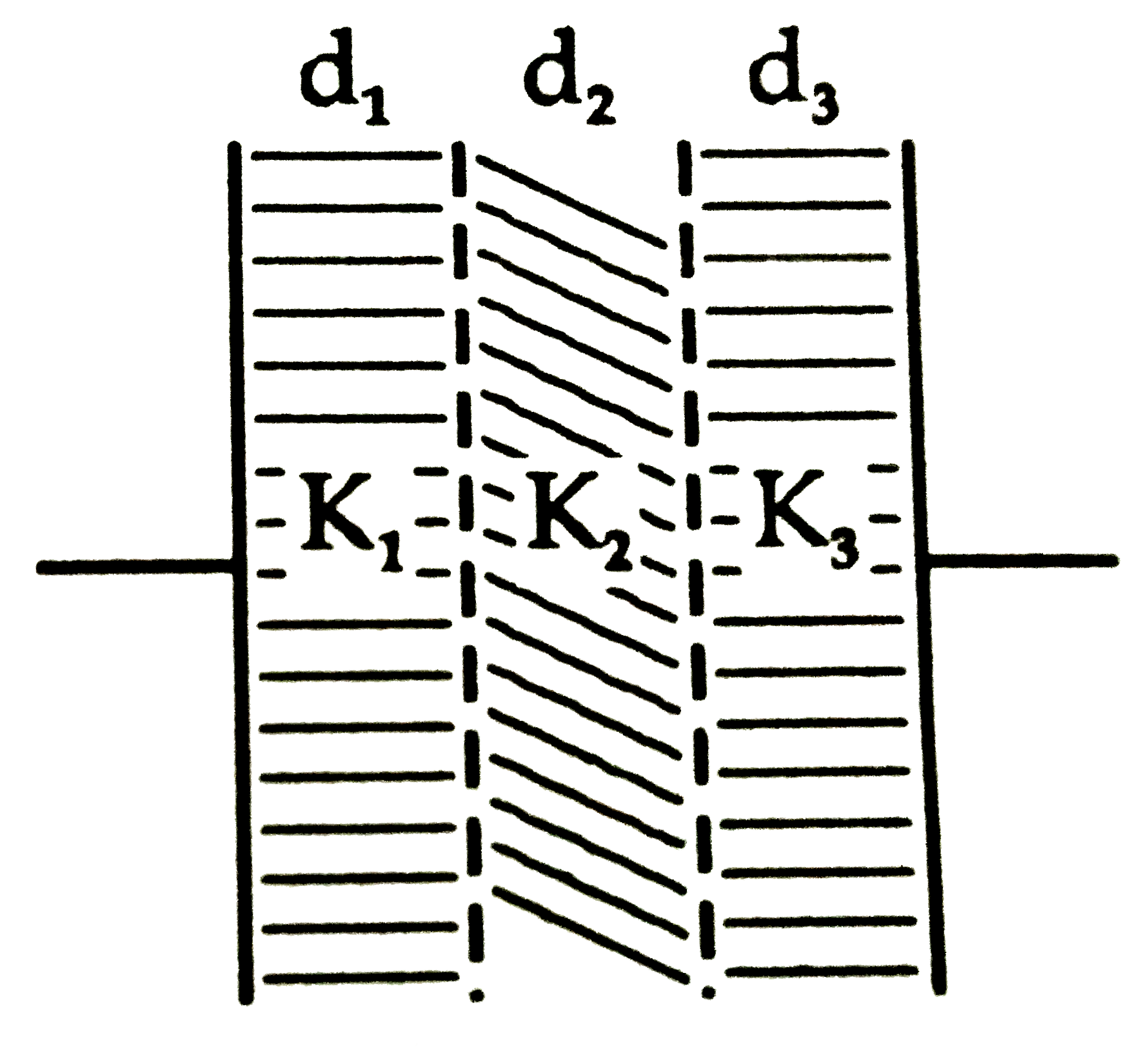
The expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure will be
A
∈0Ad1K1+d2K2+d3K3
B
∈0Ad1K1−d2K2−d3K3
C
∈0A2d1K1−d2K2−d3K3
D
∈0A21K1+1K2+1K3
Video Solution
Text Solution
The correct Answer is:A
The given capacitor may be supposed to be formed of three component capacitors C1,C2andC3 connected in series.
1Cs=1C1+1C2+1C3
=d1AK1∈0+d2AK2∈0+d3AK3∈0
Cs=∈0Ad1K1+d2K2+d3K3
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The expression for the capacity of a capacitor formed by placing a compound dieletric between the plates of a parallel plate capacitor, as shown in figure , will be (Given area of plate = A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3)Force of attraction between the plates of a parallel plate capacitor is
Aq22ε0AKBq2ε0AKCq2ε0ADq22ε0A2KA dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases
As the distance between the plates of a parallel plate capacitor decreased
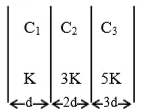
View SolutionIn the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
View SolutionIf the distance between the plates of a parallel plate capacitor of capacity of μF is doubled, then new capacity will be
View SolutionIf the distance between the plates of a parallel plate capacitor of capacity 10μF is doubled, then new capacity will be
View SolutionIn a parallel plate capacitor , the capacity increases if
View Solution

