The space between parallel plate capacitors is filled with four dielectrics of equal dimensions but of dielectric constants K1,K2,K3andK4 respectively. If K is the dielectric constant of a single dielectric that must be filled between capacitor plates to have the same capacitance between A and B. Then we must have

1K=1K1+K2+1K3+K4
1K=1K1+K2−1K3+K4
1K=1K1−K2+1K3−K4
1K=1K1−K2−1K3−K4
The correct Answer is:A
The given capacitor may be supposed to be formed of four component capacitors C1,C2,C3andC4. The capacitor C1andC2 are in parallel and C3andC4 are in parallel.
From figure,
C1=AK1∈02d/2=A∈0K1d
C2=A∈0K2d
C3=A∈0K3d
C4=A∈0K4d
Now,
1C=1CP1+1CP2
1C=1C1+C2+1C3+C4
1AK∈0d=1A∈0dK1+A∈0dK2+1A∈0dK3+A∈0dK4
1K=1K1+K2+1K3+K4
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
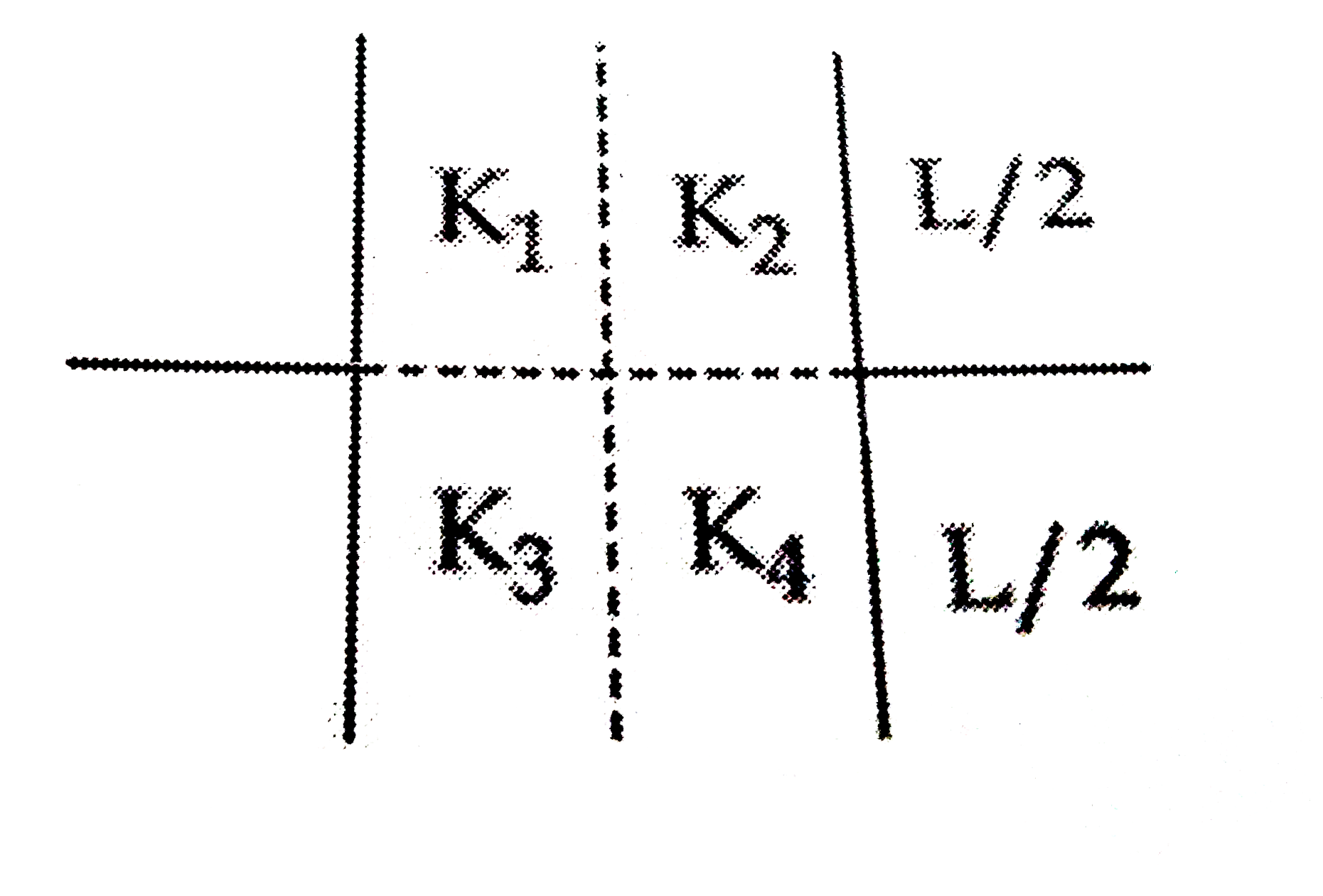
View SolutionThe area A of a parallel plate capacitor is divided into two equal, halves and filled with two media of dielectric constants K1andK2 respectively. The capacitance of the capacitor will be

View Solution
Knowledge Check
A parallel plate capacitor is filled with dielectrics. What is capacitance?
 A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)
A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
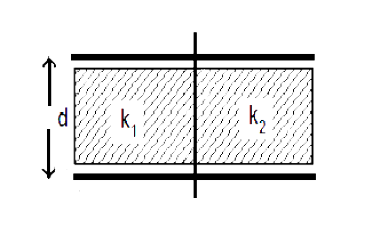 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)A parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by
 AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
A parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
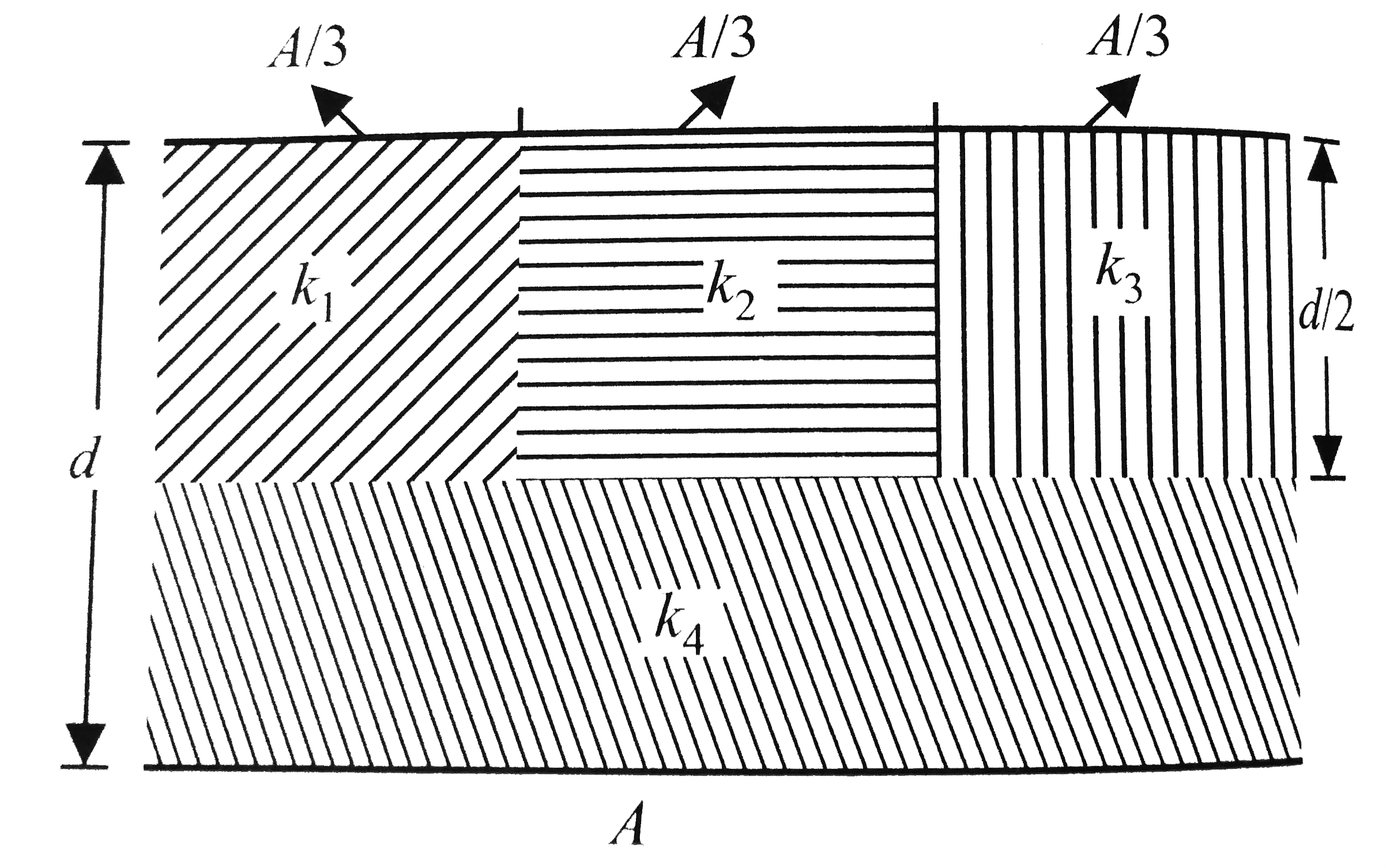
View SolutionA parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by

View SolutionA parallel plate condenser is filled with two dielectrics as shown. Area of each plate is Ametre2 and the separtion is t metre. The dielectric constants are K1 and K2, respectively. Its capacitance in farad will be

View SolutionIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
View SolutionHalf of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
View Solution

