If the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
Increases by a factor 2
Increases by a factor √2
Decreased by a factor √2
Decreased by a factor 1/2
The correct Answer is:d
To solve the problem of finding the electric field between the plates of a parallel plate capacitor when a dielectric medium with a dielectric constant k=2 is introduced, we can follow these steps:
Step 1: Understand the Initial Condition
Initially, we have a parallel plate capacitor with air (or vacuum) between the plates. The electric field E in this case can be expressed as:
E=QAϵ0
where Q is the charge on one plate, A is the area of the plates, and ϵ0 is the permittivity of free space.
Step 2: Introduce the Dielectric Medium
When a dielectric medium with dielectric constant k is introduced between the plates, the electric field E′ in the presence of the dielectric is given by:
E′=Ek
This means the electric field is reduced by a factor of k.
Step 3: Substitute the Dielectric Constant
Given that the dielectric constant k=2, we can substitute this value into the equation:
E′=E2
Step 4: Relate the New Electric Field to the Original Electric Field
Since we already established that the original electric field E is:
E=QAϵ0
We can express the new electric field as:
E′=12⋅QAϵ0
Step 5: Conclusion
Thus, the electric field between the plates when the dielectric medium is introduced is reduced by a factor of 2:
E′=E2
Final Answer
The electric field between the plates is decreased by a factor of 2.
---
Initially, we have a parallel plate capacitor with air (or vacuum) between the plates. The electric field E in this case can be expressed as:
E=QAϵ0
where Q is the charge on one plate, A is the area of the plates, and ϵ0 is the permittivity of free space.
When a dielectric medium with dielectric constant k is introduced between the plates, the electric field E′ in the presence of the dielectric is given by:
E′=Ek
This means the electric field is reduced by a factor of k.
Given that the dielectric constant k=2, we can substitute this value into the equation:
E′=E2
Since we already established that the original electric field E is:
E=QAϵ0
We can express the new electric field as:
E′=12⋅QAϵ0
Thus, the electric field between the plates when the dielectric medium is introduced is reduced by a factor of 2:
E′=E2
The electric field between the plates is decreased by a factor of 2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - WB JEE / WORKOUT) CATEGORY 2 : Single Option Correct Type (2 Marks)
15 Videos
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE / WORKOUT )CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
10 Videos
- ELECTROMAGNETIC WAVES BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC WAVES EXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
- GRAVITATIONBOOK - MTG-WBJEECHAPTER - GRAVITATIONEXERCISE - WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
7 Videos
Similar Questions
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionHalf of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
View Solution
Knowledge Check
The gap between the plates of a parallel plate capacitor is filled with glass of dielectric constant k=6 and of specific resistivity 100GΩm. The capacitance of the capacitor is 4.0mF. When a voltage of 2.0kV is applied to the capacitor, the leakage current of the capacitor will be.
A2.0×10−6AB3.0×10−6AC1.5×10−3ADZeroIn figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A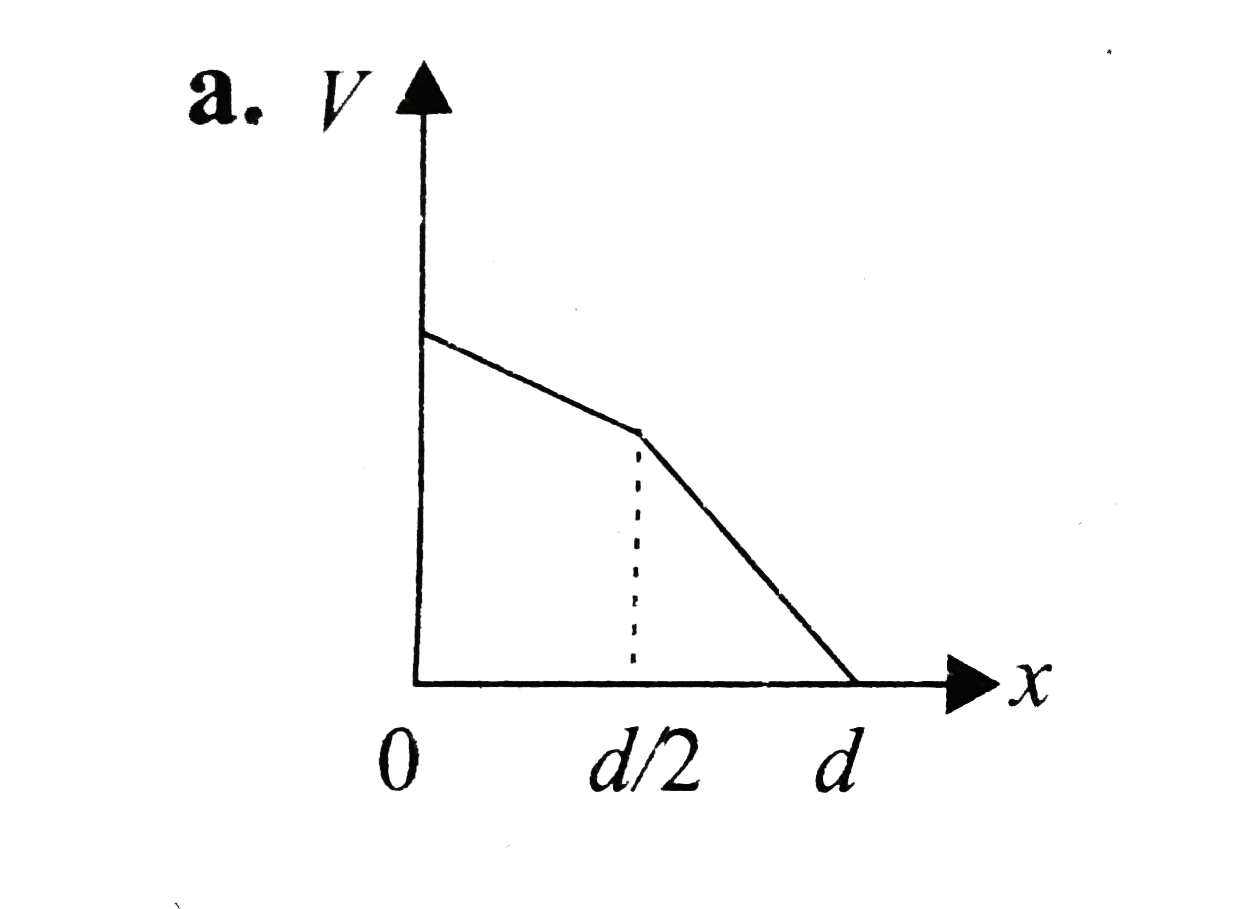 B
B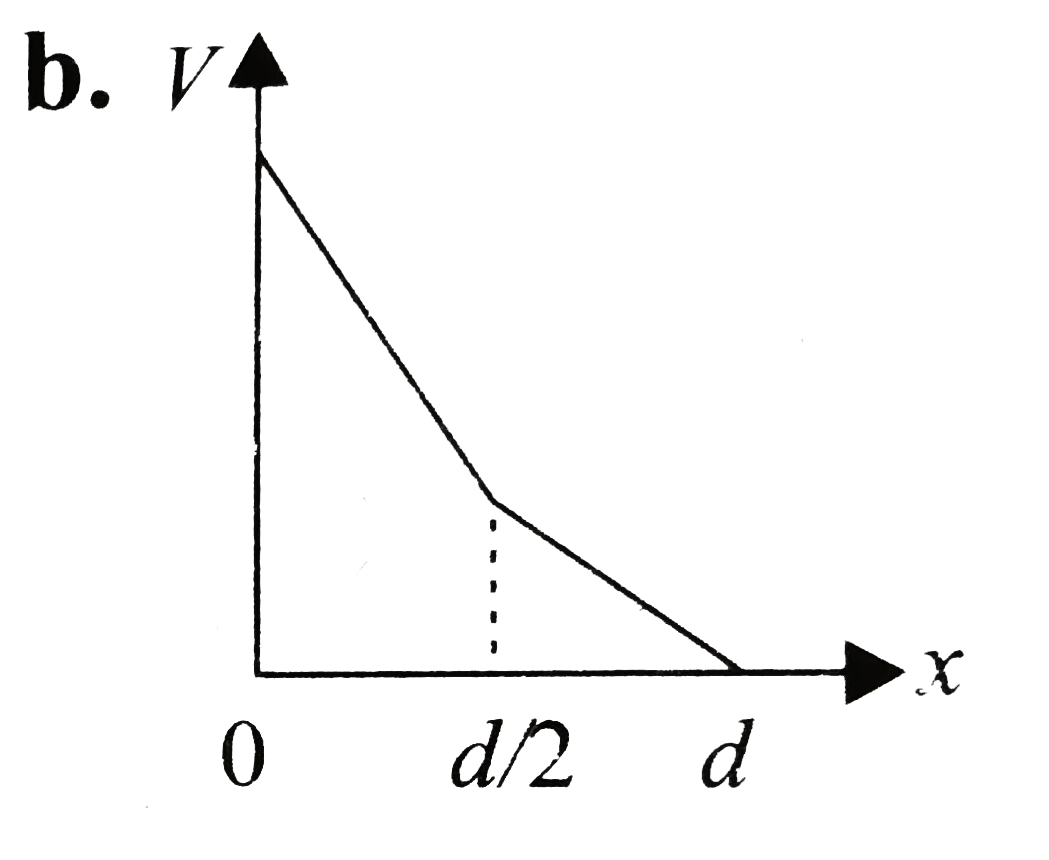 C
C D
D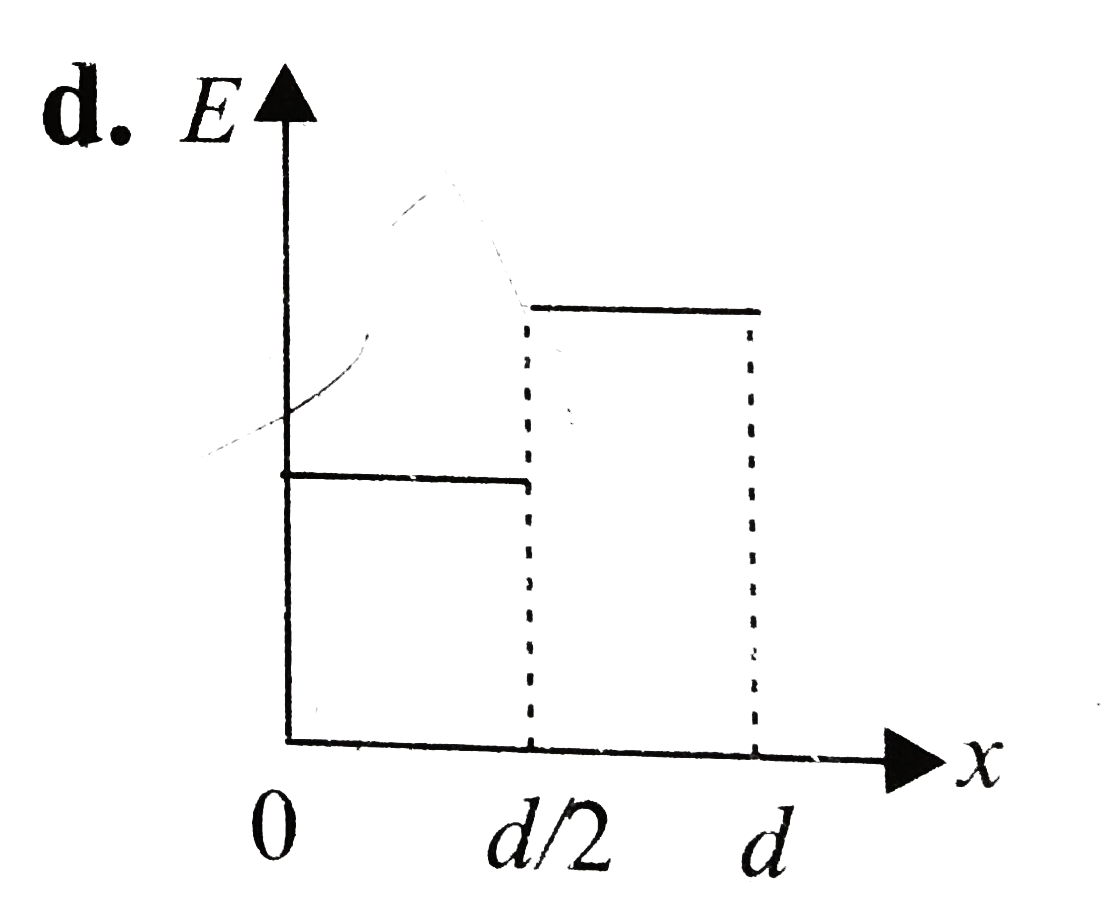
Half of the space between the plates of a parallel plate capacitor is filled with a dielectric material of dielectric constant K . The ramaining half contains air as shown in the figure . The capacitor is now given a charge Q . Then
 Aelectric field in the dielectric filled region is higher than that in the air - filled region.Bon the two halves of the bottom plate the charge densities are unequal.Ccharge on the half of the top plate above the air filled part is QK+1.Dcapacitance of the capacitor shown above is (1+K)C02, where C0 is the capacitance of the same capacitor with dielectric removed.
Aelectric field in the dielectric filled region is higher than that in the air - filled region.Bon the two halves of the bottom plate the charge densities are unequal.Ccharge on the half of the top plate above the air filled part is QK+1.Dcapacitance of the capacitor shown above is (1+K)C02, where C0 is the capacitance of the same capacitor with dielectric removed.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is
View SolutionIf the distance between the plates of parallel plate capacitor is halved and the dielectric constant of dielectric is doubled, then its capacity will
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor is charged completely and then disconnected from the battery. IF the separation between the plates is reduced by 50% and the space between the plates if filled with a dielectric slab of dielectric constant 10, then the potential difference between the plates
View SolutionConsider a parallel plate capacitor of 10μF with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to

View Solution
