A 900 pF capacitor is charged by a 100 V battery. The electrostatic energy stored by the capacitor is
9×105J
4.5×10−6J
2.2×10−6J
9×10−10J
The correct Answer is:B
To find the electrostatic energy stored in a capacitor, we can use the formula:
U=12CV2
where:
- U is the electrostatic energy,
- C is the capacitance in Farads,
- V is the voltage in Volts.
Step 1: Convert the capacitance from picoFarads to Farads.
Given:
- Capacitance C=900pF
To convert picoFarads to Farads:
C=900pF=900×10−12F
Step 2: Identify the voltage.
Given:
- Voltage V=100V
Step 3: Substitute the values into the energy formula.
Using the formula:
U=12CV2
Substituting the values:
U=12×(900×10−12)×(100)2
Step 4: Calculate V2.
Calculating V2:
V2=1002=10000
Step 5: Substitute V2 back into the equation.
Now substituting V2 into the equation:
U=12×(900×10−12)×10000
Step 6: Simplify the expression.
Calculating:
U=12×(900×10−12)×(104)
U=12×(900×10−8)J
U=450×10−8J
Step 7: Convert to standard form.
U=4.5×10−6J
Final Answer:
The electrostatic energy stored by the capacitor is 4.5×10−6J or 4.5μJ.
- U is the electrostatic energy,
- C is the capacitance in Farads,
- V is the voltage in Volts.
- Capacitance C=900pF
C=900pF=900×10−12F
- Voltage V=100V
U=12CV2
U=12×(900×10−12)×(100)2
V2=1002=10000
U=12×(900×10−12)×10000
U=12×(900×10−12)×(104)
U=12×(900×10−8)J
U=450×10−8J
The electrostatic energy stored by the capacitor is 4.5×10−6J or 4.5μJ.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Fill in the Blanks)
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Short Answer Questions)
Explore 38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Very Short Answer Questions)
Explore 56 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
A 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?
View Solution(a) A parallel plate capacitor has a capacity of 6μF, with air in between the plates and 60μF when dielectric medium is introduced. What is the dielectric constant (K) of the medium?
(b) A 900 pF capacitor is charged by 100 V battery.
(i) How much electrostatic energy is stored by the capacitor?
(ii) The capacitor is now disconected from the battery and is connected to another uncharged 900 pF capacitor. How much is the electrostatic energy stored in the system?
View Solution
Knowledge Check
A 700 pF capacitor is charged by a 50 V battery. The electrostatic energy stored it is
A17.0×10−8JB13.6×10−9JC9.5×10−9JD8.7×10−7JA capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
A 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?
View SolutionThe total electrostatic energy stored in both the capacitor is
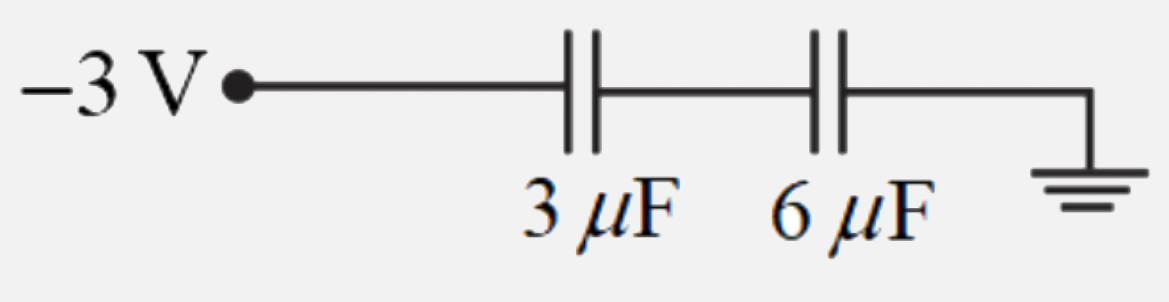
View SolutionA 12pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ? If another capacitor of 6pF is connected across the combination, find the charge stored and potential difference across each capacitor.
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionA 2μF capacitor is connected to a 10 V battery. What is the electrostatic energy stored in the capacitor?
View Solution

