A parallel plate capacitor with a dielectric slab with dielectric constant k=3 filling the space between the plates is charged to potential V and isolated. Then the dielectric slab is drawn out and another dielectric slab of equal thickness but dielectric constant k'=2 is introduced between the plates. The ratio of the energy stored in the capacitor later to that initially is:
2:3
3:2
4:9
9:4
The correct Answer is:B
To find the ratio of the energy stored in the capacitor after the dielectric slab is changed to that initially, we will follow these steps:
1. Identify Initial Conditions:
- The initial dielectric constant k=3.
- The capacitor is charged to a potential V and is isolated.
2. Calculate Initial Capacitance:
- The capacitance C1 of the capacitor with the dielectric is given by:
C1=k⋅A⋅ϵ0d=3⋅A⋅ϵ0d
3. Calculate Initial Charge:
- The charge Q on the capacitor is:
Q=C1⋅V=3⋅A⋅ϵ0d⋅V
4. Calculate Initial Energy:
- The energy E1 stored in the capacitor is given by:
E1=Q22C1=Q22⋅3⋅A⋅ϵ0d=Q2⋅d6⋅A⋅ϵ0
5. Change Dielectric:
- The dielectric slab is removed and replaced with a new slab of dielectric constant k′=2.
6. Calculate New Capacitance:
- The new capacitance C2 is given by:
C2=k′⋅A⋅ϵ0d=2⋅A⋅ϵ0d
7. Charge Remains Constant:
- Since the capacitor is isolated, the charge Q remains the same.
8. Calculate New Energy:
- The new energy E2 stored in the capacitor is:
E2=Q22C2=Q22⋅2⋅A⋅ϵ0d=Q2⋅d4⋅A⋅ϵ0
9. Calculate the Ratio of Energies:
- The ratio of the energy stored in the capacitor later to that initially is:
E2E1=Q2⋅d4⋅A⋅ϵ0Q2⋅d6⋅A⋅ϵ0=64=32
Final Answer:
The ratio of the energy stored in the capacitor later to that initially is 32.
- The initial dielectric constant k=3.
- The capacitor is charged to a potential V and is isolated.
- The capacitance C1 of the capacitor with the dielectric is given by:
C1=k⋅A⋅ϵ0d=3⋅A⋅ϵ0d
- The charge Q on the capacitor is:
Q=C1⋅V=3⋅A⋅ϵ0d⋅V
- The energy E1 stored in the capacitor is given by:
E1=Q22C1=Q22⋅3⋅A⋅ϵ0d=Q2⋅d6⋅A⋅ϵ0
- The dielectric slab is removed and replaced with a new slab of dielectric constant k′=2.
- The new capacitance C2 is given by:
C2=k′⋅A⋅ϵ0d=2⋅A⋅ϵ0d
- Since the capacitor is isolated, the charge Q remains the same.
- The new energy E2 stored in the capacitor is:
E2=Q22C2=Q22⋅2⋅A⋅ϵ0d=Q2⋅d4⋅A⋅ϵ0
- The ratio of the energy stored in the capacitor later to that initially is:
E2E1=Q2⋅d4⋅A⋅ϵ0Q2⋅d6⋅A⋅ϵ0=64=32
The ratio of the energy stored in the capacitor later to that initially is 32.
Topper's Solved these Questions
- CAPACITANCEBook:PHYSICS GALAXY - ASHISH ARORAChapter:CAPACITANCEExercise:NUMERICAL MCQS
Explore 56 Videos
- CAPACITANCEBook:PHYSICS GALAXY - ASHISH ARORAChapter:CAPACITANCEExercise:ADVANCE MCQS
Explore 26 Videos
- CAPACITANCEBook:PHYSICS GALAXY - ASHISH ARORAChapter:CAPACITANCEExercise:DISCUSSION QUESTIONS
Explore 22 Videos
- ATOMIC PHYSICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ATOMIC PHYSICSExercise:Unsolved Numerical Problems
Explore 39 Videos
- CURRENT ELECTRICITYBook:PHYSICS GALAXY - ASHISH ARORAChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 389 Videos
Similar Questions
A dielectric of dielectric constant 3 fill up three fourths of the space between the plates of a paralleled plate capacitor. The fraction of total energy that is stored in the dielectric is
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
electric filed intensity between the plates ? Justify your answer .
View Solution
Knowledge Check
A parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
Athe stored energy remains unchanged.Bthe stored energy is increased by a factor of 2.Cthe stored energy is reduced to half its previous value.Dnone of the above is correct.If a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
A1. decreasedB2. unaffectedC3. almost halvedD4. almost doubledThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
Aε0Ad−x(1−1K)Bε0Ad+x(1−1K)Cε0Ad+x(1+1K)Dε0Ad−x(1+2K)
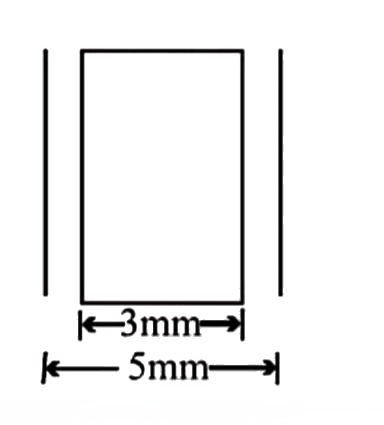
Separation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionA parallel plate capacitor has a capacity c. If a medium of dielectric constant K is introduced between plates, the capacity of capacitor becomes
View SolutionA parallel plate copacitor is first charged and then isolated, and a dielelctric slab is introduced between the plates. The quantity that remains unchanged is.
View SolutionA parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
View SolutionThe plates of a capacitor are connected to a source of emf and the energy stored is U0. When dielectric material dielectric constant K is introduced between the plates filling the whole space, the energy stored becomes U Now.
View Solution

