Inside a ball charged uniformly with volume density ρ there is a spherical cavity. The centre of the ball by a distance a. Find the field strength E inside the cavity, assuming the permittively equal to unity.
Using Gauss theroem we can easily show that the electric field strength within a uniformly, charged sphere is →E=(ρ3ε0)→r
The cavity in out problem, may be considered as the superpositon of two balls, one with the charge density ρ and the other with ρ.
Let P be a point inside the cavity such that its position vector with respect with respect to the centre of cavity to →r adn with respect to the centre of the ball →r+. Then from the principle of superpositon, field inside the cavity at an arbitary point P,
→E=−−→E++−−→E−
=ρ3ε0(−→r+−−→r−)=ρ3ε0→a
Note : Obtained expression for →E shows that it is valid regarless of the ratio between the radii of the sphere and the distance between their centires.

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Conductors And Dielectrics In An Electric Field
Explore 47 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View SolutionInside a indinitely long circular cylinder cavity. The distance between the axes of the cylinder and the cavity is equal to a. Find the electric field strength E inside the cavity. The permittivity is assumed to eb equal to unity.
View Solution
Knowledge Check
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2A metallic ball has spherical cavity at its centre. If the ball is heated, what happens to the cavity
AIts volume decreases.BIts volume remains constant.CIts volume increases.DNothing can be decided.A solid metal ball has a spherical cavity. If the ball is heatd, the volume of the cavity will
AincreaseBdecreaseCremain unffecetedDremain unaffected but the sphere of the cavity will change
A sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

View SolutionA non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density ρ=kr2 where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre?
View SolutionA system consits of a ball of radus R carrying spherically symmetric charge and the surrounding space filled with a charge of volume density ρ=α/r , wehre α is a constant, r is the distance from the centre of the ball. Find the ball's the charge at whcih the magnitude of the electric field strength vector is independent of r outside the ball. How high is this strength ? The permittives of the ball and the surrounding space are assumed to be equal to unity.
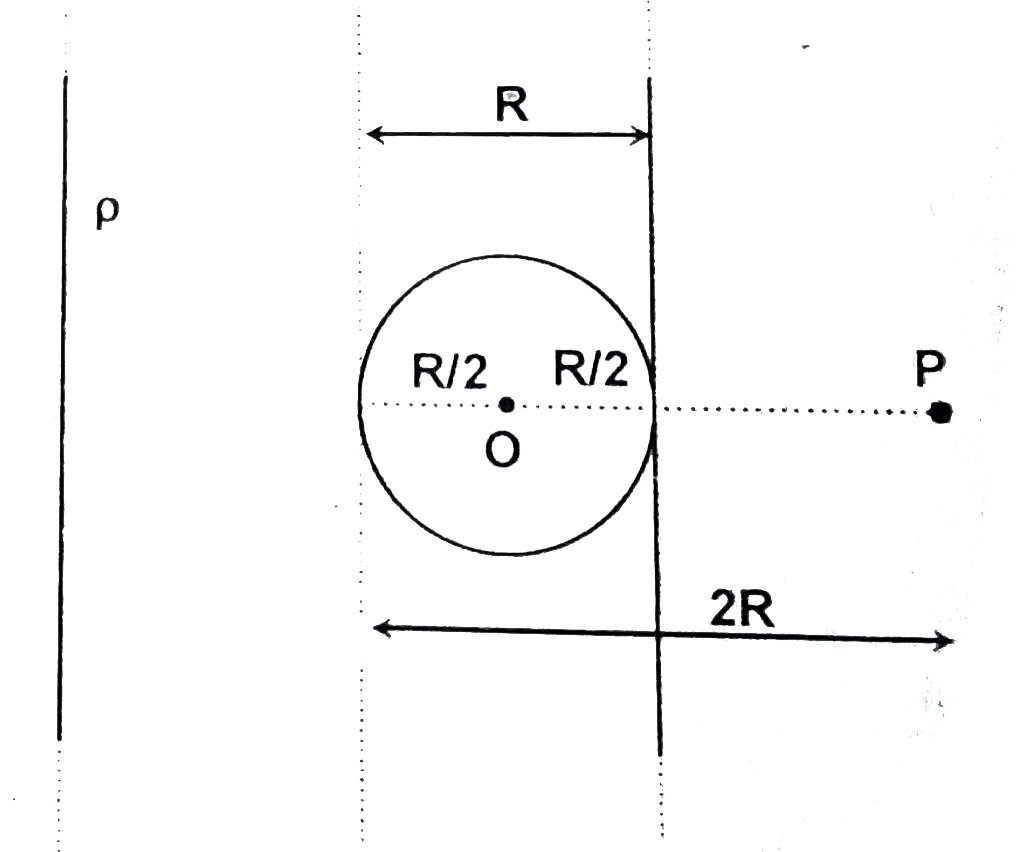
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
View SolutionChoose the most appropriate option.
A metallic ball has spherical cavity at its centre. If the ball is heated, what happens to the cavity?
View Solution

