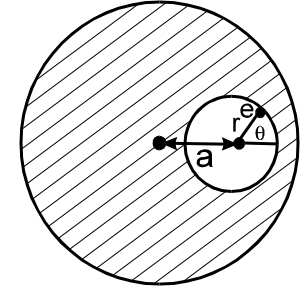
Inside a indinitely long circular cylinder cavity. The distance between the axes of the cylinder and the cavity is equal to $a$ . Find the electric field strength $E$ inside the cavity. The permittivity is assumed to eb equal to unity.

Video Solution

Text Solution

Verified by Experts

Let us consider a cylindrical Gaussain surface of radius $r$ and height $h$ inside an infinitely long charged cylinder with charge density $ρ$ . Now from Gauss theroem :
$E_{r} 2 π r h = \frac{q_{inclosed}}{ε_{0}}$
(where $E_{r}$ is the field inside the cylinder at a distance $r$ from its axis.)
or, $E_{r} = 2 π r h = \frac{ρ π r^{2} h}{ε_{0}}$ or $E_{r} = \frac{ρ r}{2 ε_{0}}$
Now, using the method of $3.28$ field at point $P$ , inside the cavity, is
$\to E = - - \to E_{+} + - - \to E_{-} = \frac{ρ}{2 ε_{0}} (- \to r_{+} - - \to r_{-}) = \frac{ρ}{2 ε_{0}} \to a$

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Knowledge Check

A long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure

The magnetic induction at point on the cavity is
A $\frac{μ_{0} I}{3 π R} (- ˆ l)$
B $\frac{μ_{0} i}{3 π R} (ˆ k)$
C $\frac{μ_{0} i}{6 π R} (ˆ j)$
D $\frac{μ_{0} I}{6 π R} (- ˆ j)$
A solid non-conducting sphere of radius R is charged with a uniform volume charge density $ρ$ . Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle $θ = 45^{\circ}$ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.

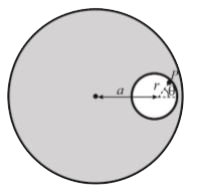A $\sqrt{\frac{3 R m ε_{0} r}{e ρ a}}$
B $\sqrt{\frac{6 m ε_{0} r}{e ρ a}}$
C $\sqrt{\frac{6 \sqrt{3} m ε_{0} R}{e ρ a}}$
D $\sqrt{\frac{6 \sqrt{2} m ε_{0} r}{e ρ a}}$
Inside a uniform sphere of density $ρ$ there is a spherical cavity whose centre is at a distance $l$ from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
A $E = \frac{- 2}{3} π G ρ l$
B $E = \frac{- 4}{3} π G ρ l$
C $E = \frac{- 4}{3} π^{2} G ρ l$
D $E = \frac{- 4}{3} π G ρ^{2} l^{2}$

IE IRODOV, LA SENA & SS KROTOV-ELECTRODYNAMICS-Motion Of Charged Particle In Magnetic Field

Home
Ask Doubt
Profile

Inside a indinitely long circular cylinder cavity. The distance between the axes of the cylinder and the cavity is equal to a. Find the electric field strength E inside the cavity. The permittivity is assumed to eb equal to unity.

Topper's Solved these Questions

Similar Questions

Knowledge Check

Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.

IE IRODOV, LA SENA & SS KROTOV-ELECTRODYNAMICS-Motion Of Charged Particle In Magnetic Field

Inside a indinitely long circular cylinder cavity. The distance between the axes of the cylinder and the cavity is equal to $a$ . Find the electric field strength $E$ inside the cavity. The permittivity is assumed to eb equal to unity.

Inside a uniform sphere of density $ρ$ there is a spherical cavity whose centre is at a distance $l$ from the centre of the sphere. Find the strength of the gravitational field inside the cavity.