A non-relativistic charged particle files through the electric field of a cyclindrical capacitor and gets into a unifrom transverse magnetic field with induction $B$ (fig). In the capacitor the particle moves along the are of a circle, in the magnetic field, along a semi-circle of radius $r$ . The potential differnce applied to the capacitor is equal to $V$ , the radii of the electrodes are equal to $a$ and $b$ , with $a < b$ . Find the velocity of the particle and its specific charge $q / m$ .

Video Solution

Text Solution

Verified by Experts

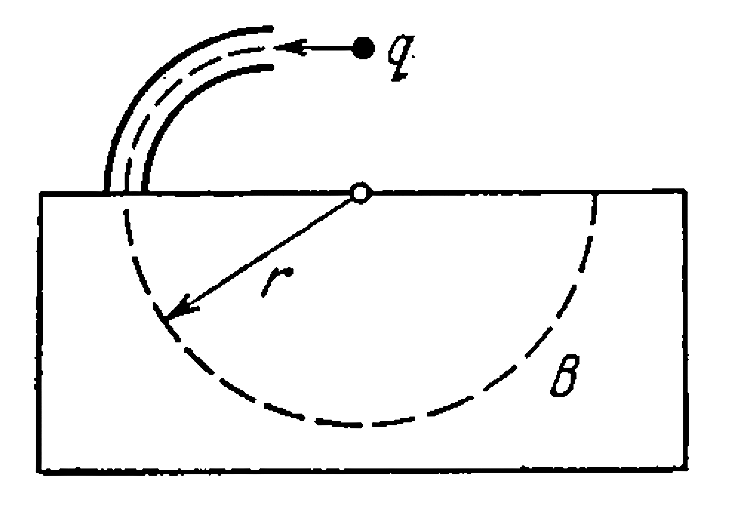
Inside the capacitor, the electric field follows $a \frac{1}{r}$ law, and so the potential can be written as
$φ = \frac{V I n r / a}{I n b / a}, E = \frac{- V}{I n b / a} \frac{1}{r}$ ,
Here $r$ is the distance from the axis of the capacitor.
Also, $\frac{m v^{2}}{r} = \frac{q V}{I n b / a r} \frac{1}{r}$ or $m v^{2} = \frac{q V}{I n b / a}$
On the other hand
$m v = q B r$ in the magentic field.
Thus, $v = \frac{V}{B r I n b / a}$ and $\frac{q}{m} = \frac{v}{B r} = \frac{V}{B^{2} r^{2} I n (b / a)}$

Updated on:21/07/2023

When a charged particle moves through a magnetic field it suffers a change in its
Aenergy
Bmass
Cspeed
Ddirection of motion
A charged particle moves through a magnetic field perpendicular to its direction. Then
AAcceleration remain unchanged
Bvelocity remains unchanged
Cspeed of the particle remains unchanged
DDirection of the particle remains unchanged
A charged particle moves through a magnetic field perpendicular to its direction. Then
Akinetic energy changes but the momentum is constant
Bthe momentum changes but the kinetic energy is constant
Cboth momentum and kinetic energy of the particle are not constant
Dboth momentum and kinetic energy of the particle are constant