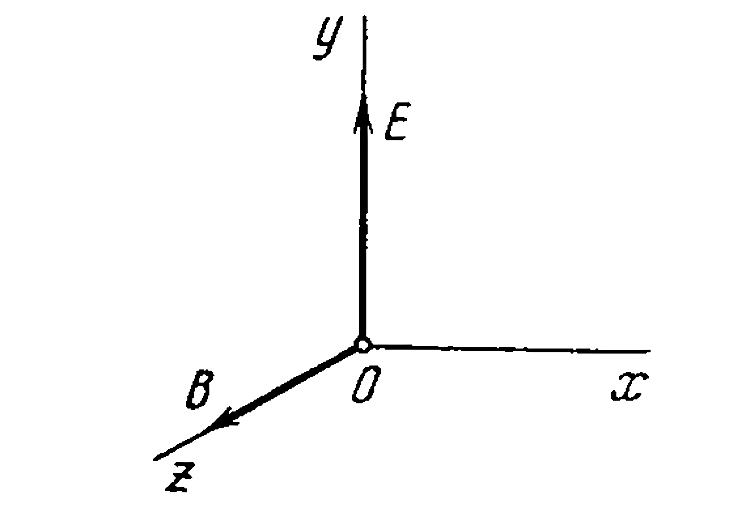
A particle with specific charge q/m moves in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with strength E and induction B (fig). At the moment t=0 the particle was located at the point O and had zero velocity. For the non-relativistic case find:
(a) the law of motion x(f) and y(t) of the particle, the shape of the trajectory,
(b) the lenght of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero,
(c) the mean value of the particle's velocity vector projections on the x axis (the drift velocity).
The equaciton of motion is,
md2→rdt2=q(→E+→v×→B)
Now, →v×→B=∣∣
∣
∣∣ˆiˆjˆk.x.y.z00B∣∣
∣
∣∣=→iB.y−→jB.x
So, the equaction becomes,
dvxdt=qBvym,dvydt=qEm−qBmvx, and dvzdt=0
Here, vx=.x,vy=.y,vz=.z. The last equactions is easy to intergate,
vz = constant = 0,
since vz is zero initially. Thus intergating again,
z = constant = 0,
and motion is condifned to the x−y plane. We now multiply the secound equaction by i and add to the first equatiion.
ξ=vx+ivy
we get the equation,
dξdt=iωξω=qBm
This equation after being mutiplied by eiωt can be rewritten as,
ddt(ξeiωt)=iωeiωtEB
and intergrated at once to give,
ξ=EB+Ce−iωt−iα,
where C and α two real constants. Taking real and imaginary parts.
vx=EB+Ccso(ωt+α) and vy=−Csin(ωt+α)
Since vy=0, when t=0, we can takek α=0, then vx=0 at t=0 gives, C=−EB we get,
vx=EB(1−cosωt) and vy=EBsinωt.
Intergating again and using x=y=0, at t=0, we get
x(t)=EB(t−sinωtω),y(t)=EωB(1−cosωt).
This is the equcation of a cycloid.
(b) The velocity is zero, when ωt=2nπ. We see that
v2=v2x+v2y=(EB)2(2−2cosωt)
pr, v=dxdt=2EB∣∣∣sinωt2∣∣∣
The quanttiy inside the modulus is positive for 0<ωt<2π. Thus we can drop the modulus and write for the distance traversed between two successikve zeroes of velocity.
S=4EωB(1−cosω2)
Putting ωt=2π, we get
S=8EωB=8mEqB2
(c) The drift velocity is the x-direction and has the magnitude,
<vs>=<EB(1−cosωt)>=EB.
Related Playlists
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
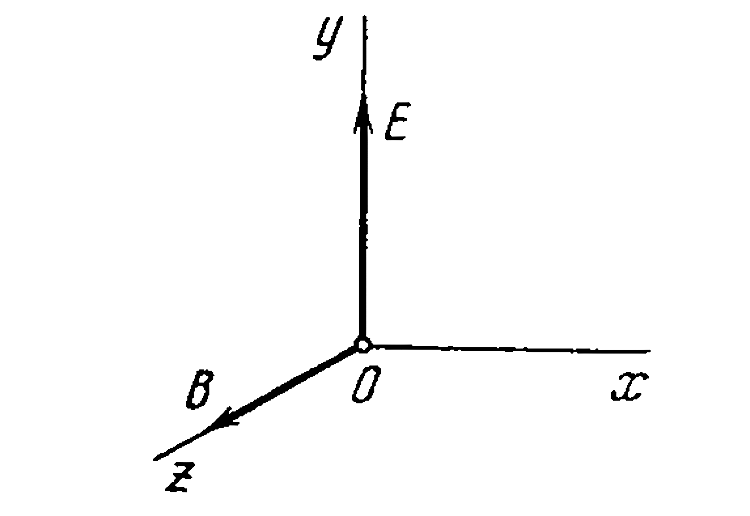
A charged particle with specfic charge q/m starts moving in the region of space where there are unifrom mutually perpendicular electric and magnitude fields. The magentic field is constant and has an induction B while the strength of the electric field varies with time as E=Emcosωt, where ω=qB/m. For the non-relativistic case find the law of motion x(t) and y(t) of the particle if at the moment t=0 it was located at the point O (see Fig). What is the appoximate shape of the trajectory of the particle?
 View Solution
View SolutionMutually perpendicular electric and magnetic fields are given by E = 1500 V/m and B = 0.04 T . Then velocity is given by
View SolutionA beam of non-relativistic charged particles moves without deviation through the region of space A where there are transverse mutually perpendicular electric and magnetic fields with strength E and induction B. When the magnetic field is switched off, the trace of the beam on the screen S shifts by Δx. Knowing the distance a and b, find the specific charge q/m of the particles.
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA beam of non-relatitivistic chagred particles moves without deviation through the region of space A (fig) where there are transerve mutually perpendicular electric and magnetic fields with streght E and induction B. When the magnetic field is swichted off, the trace of the beam on the screen S shifts by Δπ. Knowing the distances a and b, find the spefic charge q/m of the particles.
 View Solution
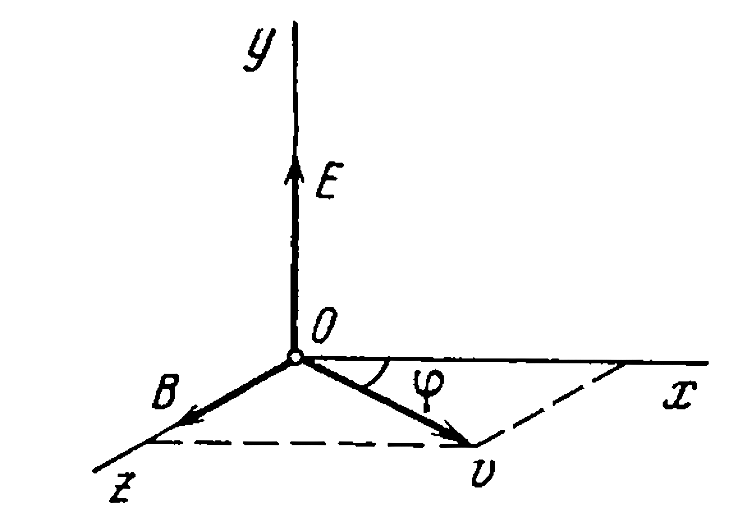
View SolutionA narrow beam of identical ions with specific charge q/m, possessing different velocities, enters the region of space, where there are unifrom parallel electric and marnetic fields the strength E and induction B, at the point O (see Fig). The beam direction coincides with the x axis at the point O. A plane screen oriented at right angles to the x axis is located at a distance l from the point O. Find the equation of the trace that the ions leave on the screen. Demonstrate that at x<<l it is the equaction of a parabola.
 View Solution
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate y_nofthepartic≤whenitcrossesthey−aξsforthen^(th) time isView SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate yn of the particle when it crosses the y-axis for the nth time isView Solution

