A sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

The electric field within the cavity or outside is the
superposition of the electric field due to the original
uncut sphere, plus the electric field due to a sphere of
the size of the cavity but with a uniform negative charge
density. The effective charge distribution is composed
of a uniformly charged sphere of radius R, charge
density ρ, superposed on it is a charge density - ρ filling
the cavity. An electric field →E1 is caused by the charge
distribution +ρ at a point →r inside the spherical cavity.
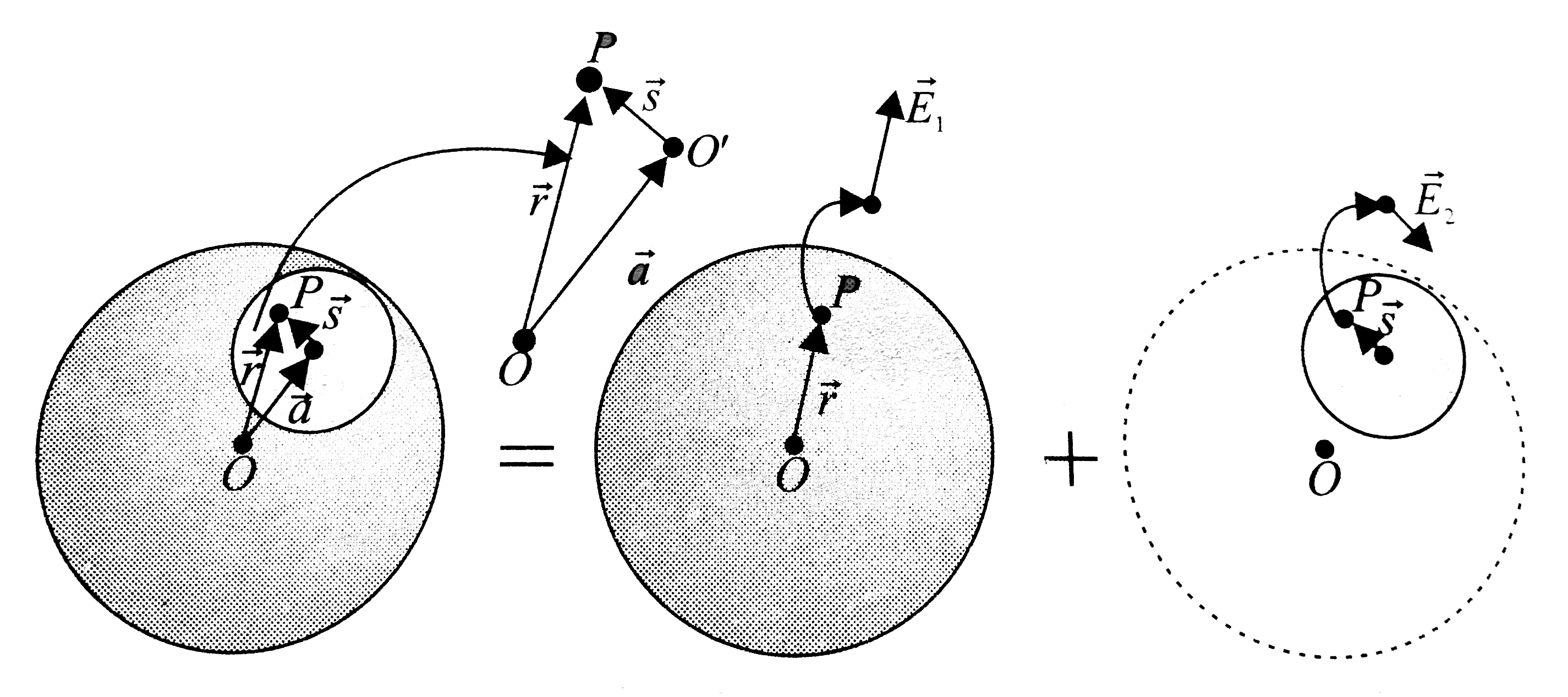
→E1=ρr3ε0r2=ρ→r3ε0
where ˆr is a unit vector in radial direction. Similarly, the electric field →E2 formed by the charge density −ρ
inside the cavity is
→E2=ρ(−→s)3ε0
Here, →s is the radius vector from the cavity centre to
the point P. From vector triangle
→r=→a+→sor→s=→r−→a
∴→E2=−ρ(→r−→a)3ε0
The resultant electric field inside the cavity is, therefore,
given by the superposition of →E1and→E2. So
→E=→E1+→E2=ρ→r3ε0+[−ρ(→r−→a)3ε0]=+ρ→a3ε0 = constant.
∴→E=ρ→a3ε0
ii. (a) Electric field at points inside the large sphere but
outside the cavity :
→E1=ρ→r3ε0
and →E2=14πε0q(−→s)s3=−(43πρb3)(→r−→a)4ε0|(→r−→a)|
The resultant electric field is
→E=→E1+→E2=ρ3ε0[→r−(b→r−→a)3(→r−→a)]
(b) Electric field at points outside the large sphere,
→E1=Qtotal)4πε0r3→r=43πR3ρ4πε0r3→r=R3ρ3ε0r3→r
→E2=Qtotal4πε0s3→s=−(43πb3ρ)4πε0(|→r−→a|)3(→r−→a)
=−ρb33ε0(|→r−→a|)3(→r−→a)
The resultant electric field is
→E=→E1+→E2=ρ3ε0[(Rr)3→r−(b→r−→a)3(→r−→a)]
∴E(→r)=⎧⎨⎩(ρ→a3ε0),⎛⎝ρ3ε0⎡⎣→r−(b|→r−→a|)3(→r−→a)⎤⎦⎞⎠,⎛⎝ρ3ε0⎡⎣(Rr)3→r−(b|→r−→a|)3(→r−→a)⎤⎦:}
Electric field inside the cavity
Electric field outside the cavity but inside the large cavity
electric field outside the large sphere .
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.2
Explore 14 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View Solution
Knowledge Check
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2A nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is
 Aρ3ε0→dBρ3ε0(→r−→d)Cρ3ε0(→d−→r)Dρ3ε0(→r)
Aρ3ε0→dBρ3ε0(→r−→d)Cρ3ε0(→d−→r)Dρ3ε0(→r)There is a uniformly charged non-conducting solid sphere. A spherical cavity is made whose centre does not coincide with the centre of solid sphere. Electric field intensity inside the cavity is
Adirectly proportional to distance of the point from centre of cavityBdirectly proportional to the distance of the point from centre of sphereCuniformDnot predictable due to insufficient information
A solid sphere ofradius 'R' is uniformly charged with charge density ρin its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. It is given that ρR2∈0=48V. Find the electric potential at the centre C of the sphere:

View SolutionDerive an expression for the electric field intensity at a point outside a charged conducting sphere.
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionA solid spherical region, having a spherical cavity whose diameter R is equal to the radius of the spherical region, has a total charge Q. Find the electric field at a point P as shown in figure
 .
.
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View Solution

