Find the electrostatic force of interaction between two halves of a spherical conductor of radius R carrying a charge Q.

Video Solution

Text Solution

Verified by Experts

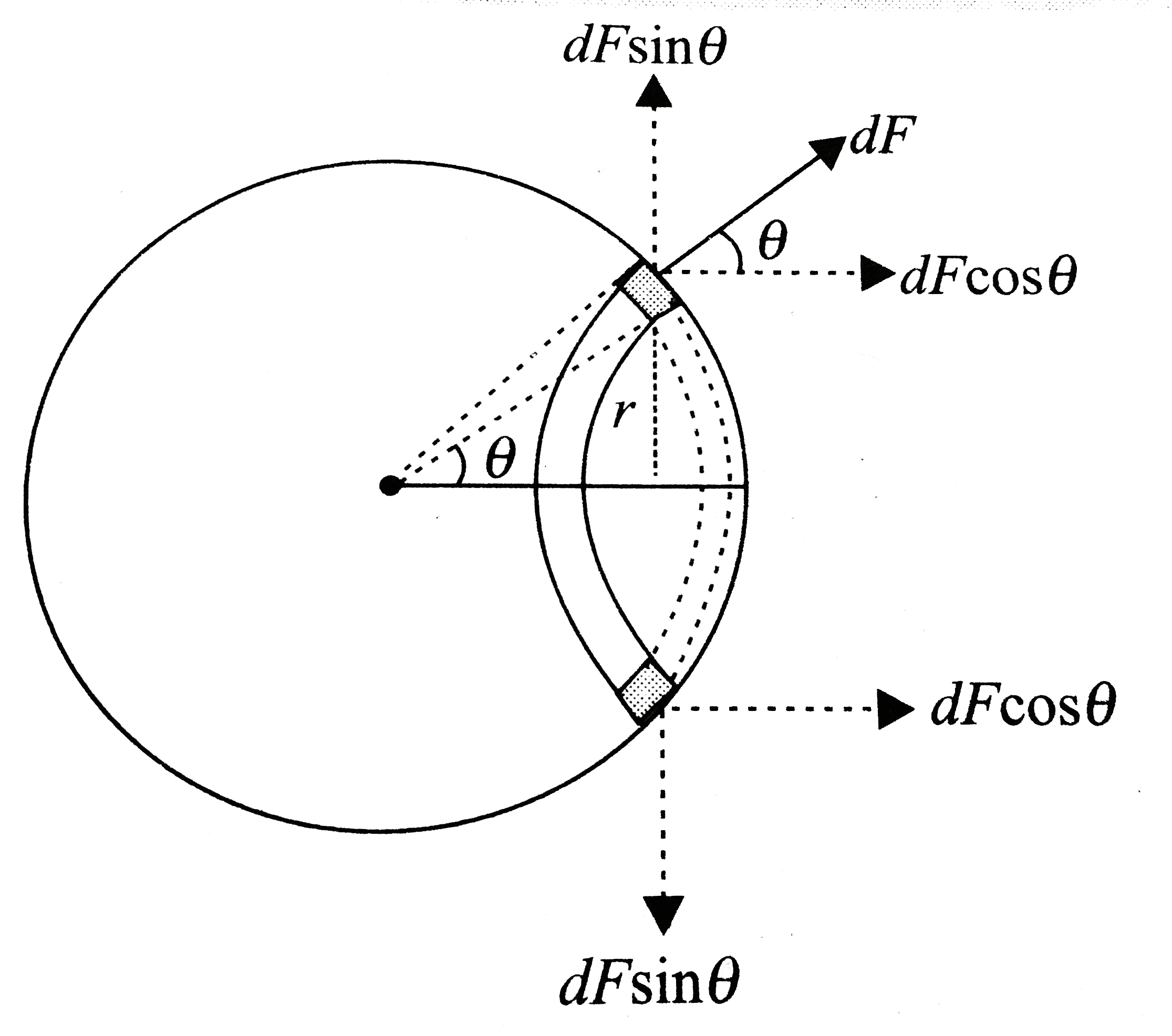
Take an elementary area dA containing a charge dq on
the elementary ring of radius r. The force acting on dq is
$d F = \frac{σ^{2}}{2 ε_{0}} d A$ (as derived earlier)
The net force on the ring is
$F_{r \in g} = \int d F sin θ = \int \frac{σ^{2}}{2 ε_{0}} d A sin θ$
$= \frac{σ^{2}}{2 ε_{0}} sin θ \int d A = \frac{σ^{2}}{2 ε_{0}} sin θ (A_{r \in g})$
where $A_{r \in g} = 2 π r d t h η = 2 π (R cos θ) R d θ = 2 π R^{2} cos θ d t h η$
or $F_{r \in g} = \frac{σ^{2} π R^{2}}{ε_{0}}$ sin theta cos theta dtheta $... ... ... . . (i) < b r >$ F_(hemisphere) = int F_(ring) $... ... ... . (i i) < b r > S u b s t i t u t \in g$ F_(ring) $o m E q . (i i), w e \geq t < b r >$ F_(hemisphere) = (sigma^2piR^2)/epsilon_0 $\in$ t_(0)^(+pi//2) $sin θ cos θ, w h e r e σ$ = Q/(4piR^2) $< b r >$ = (Q^2)/(32piepsilon_0R)

Updated on:21/07/2023

The electric field intensity at a point located at distance $r (r < R)$ from the center of a spherical conductor (radius R) charged Q will be-
A $k Q R / r^{3}$
B $k Q r / R^{3}$
C $k Q / r^{2}$
Dzero
A charged spherical conductor of radius $a$ and charge $q$ is, surrounded by another charged concentric sphere of radius $b (b > a)$ . The potential differece between conductors is $V$ . When, the spherical conductor of radius $b$ is discharged completely, then the potential difference between conductor will be
A $V$
B $\frac{V_{a}}{b}$
C $\frac{q_{1}}{4 π ε_{0} a} - \frac{q_{2}}{4 π ε_{0} b}$
DNone of the above
$A s s e r t i o n$ . Water is specially effective in screeniing the electrostatic interactions between the dissolved ions
$R e a s o n$ . The electrostatic forces between two charged ions are inversely proportional to the dielectic constant of the solvent .
AIf both assertion and reason are correct, and reason is the correct explanation of the assertion.
BIf both assertion and reason are correct , but reason is not the correct explanation of the assertion.
CIf assertion is correct, but reason is incorrect .
DIf both assertion and reason are incorrect.