The electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
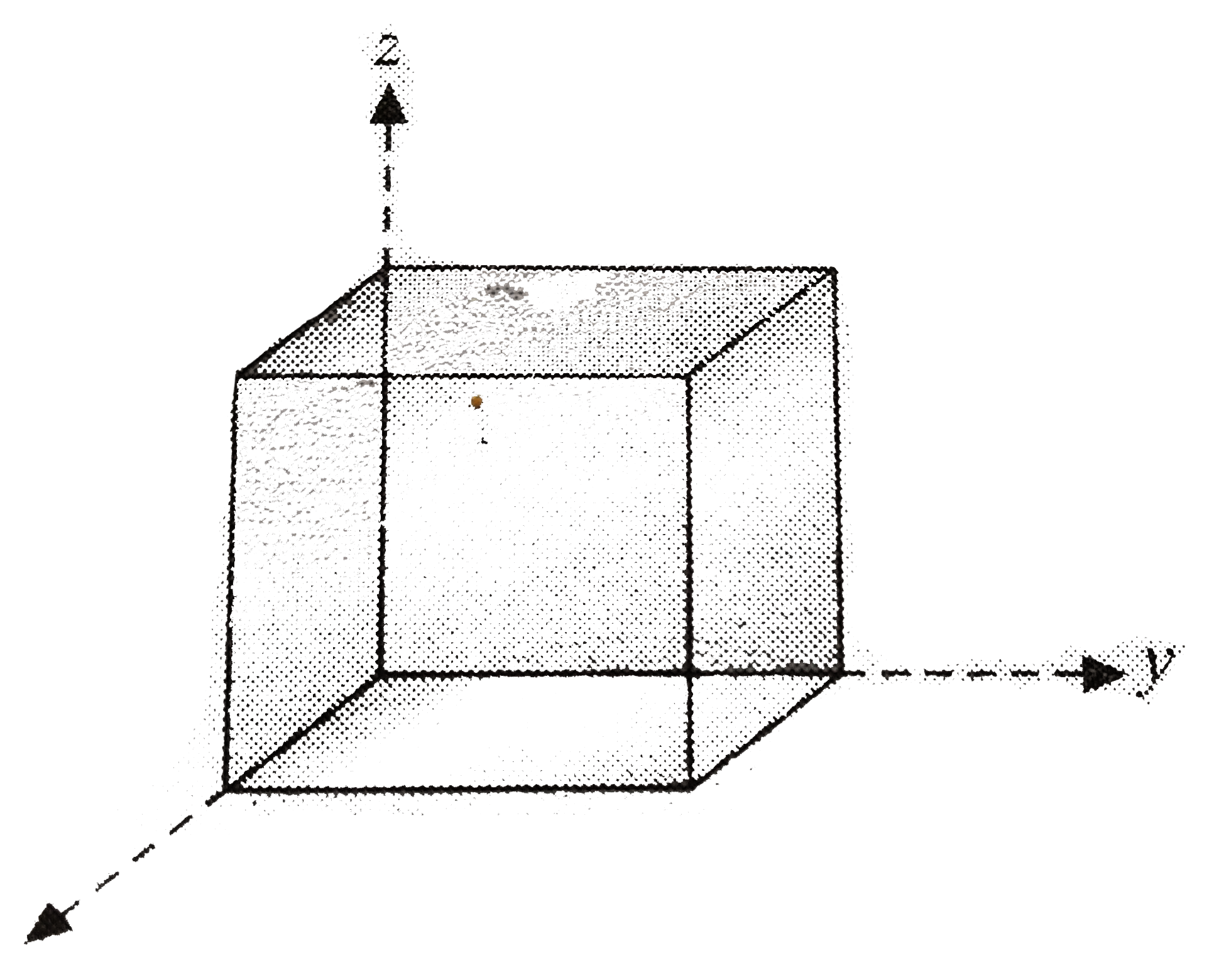
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.


We choose a differential slab of thickness dz at a distance z from
the y-axis. The electric field varies with the z-coordinate only.
The field components at this position have constant magnitude.
Consider faces 1 and 3. Net flux due to the y-component of the
field is zero (area vector and field vector are perpendicular )and
net flux due to the x-component is also zero because the net
flux in through face 3 is equal to the net flux out through face
1. Similarly, net flux through faces 2 and 4 is also zero. Flux
through each differential slab in the cube is zero. Therefore,
from Gauss's law, net charge enclosed by cubical volume is
zero.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.2
Explore 14 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
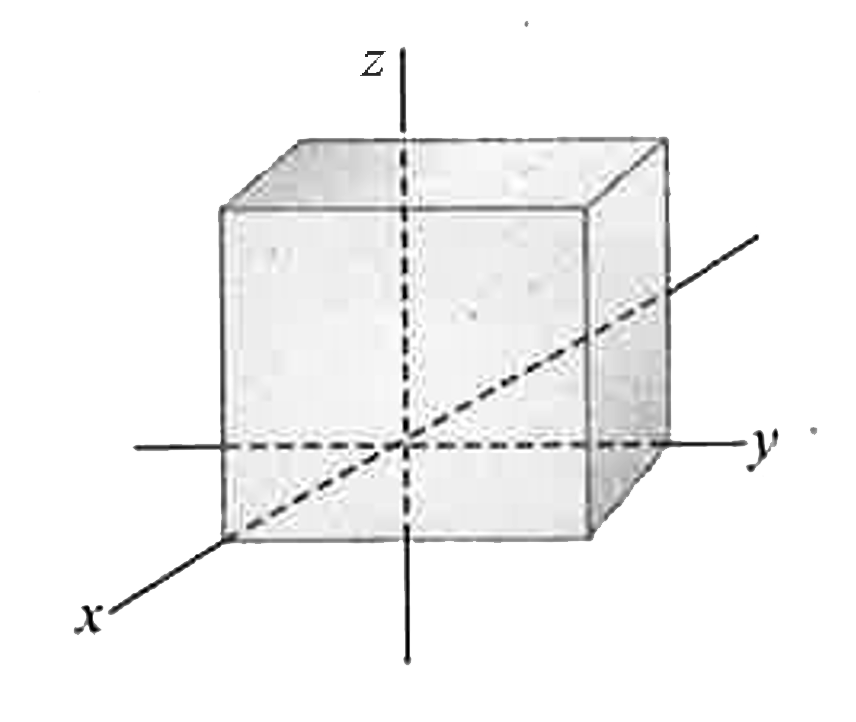
At each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
View SolutionAn electric field given by →E=4ˆi+3(y2+2)ˆj pierces a gaussian cube of side 1m placed at origin such that one of its corners is at origin and rest of sides are along positive side of coordinate axis. Find the magnitude of net charge enclosed within the cube
[3∈0]
View Solution
Knowledge Check
Electric field in EM waves is E=E0sin(kz−ωt)(ˆi+ˆj), then equation of magnetic field is:
AB=B0(−ˆi+ˆj)sin(kZ−ωt)BB=Bc(ˆi+ˆj)sin(kZ−ωt)CB=Bc(−ˆj+ˆk)sin(kZ−ωt)DB=B0(ˆi+ˆj)sin(kZ−ωt)In a region of space the electric field in the x-direction and proportional to xi.e., →E=E0xˆi. Consider an imaginary cubical volume of edge a with its sides parallel to the axes of coordinates. The charge inside this volume will be
AzeroBε0E0a3C1ε0E0a3D16ε0E0a3Uniform electric field exists in a region and is given by →E=E0ˆi+E0ˆj. There are four points A(−a,0),B(0,−a),C(a,0),andD(0,a) in the xy plane. Which of the following is the correct relation for the electirc potential?
AVA=VC>VB=VDBVA=VB>VC=VDCVA>VC>VB=VDDVA<VC<VB<VD
An electric field given by →E=4ˆi−(20y2+2)ˆj pierces a Gussian cube of side 1 m placed at origin such that its three sides represents x,y and z axes. The net charge enclosed within the cube is x×10−10C, where is _____. (take ∈0=8.85×10−12N−1m−2C2)
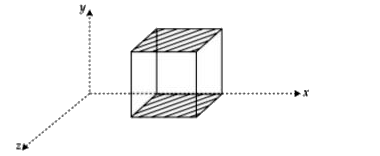
View SolutionA cube is placed inside an electric field, →E=150y2ˆj. The side of the cube is 0.5 m and is placed in the field as shown in the given figure. The charge inside the cube is :
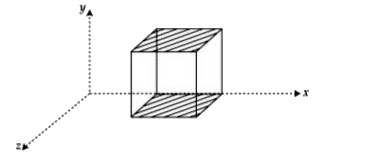
View SolutionA cube is placed inside an electric field, →E=150y2ˆj. The side of the cube is 0.5 m and is placed in the field as shown in the given figure. The charge inside the cube is :
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
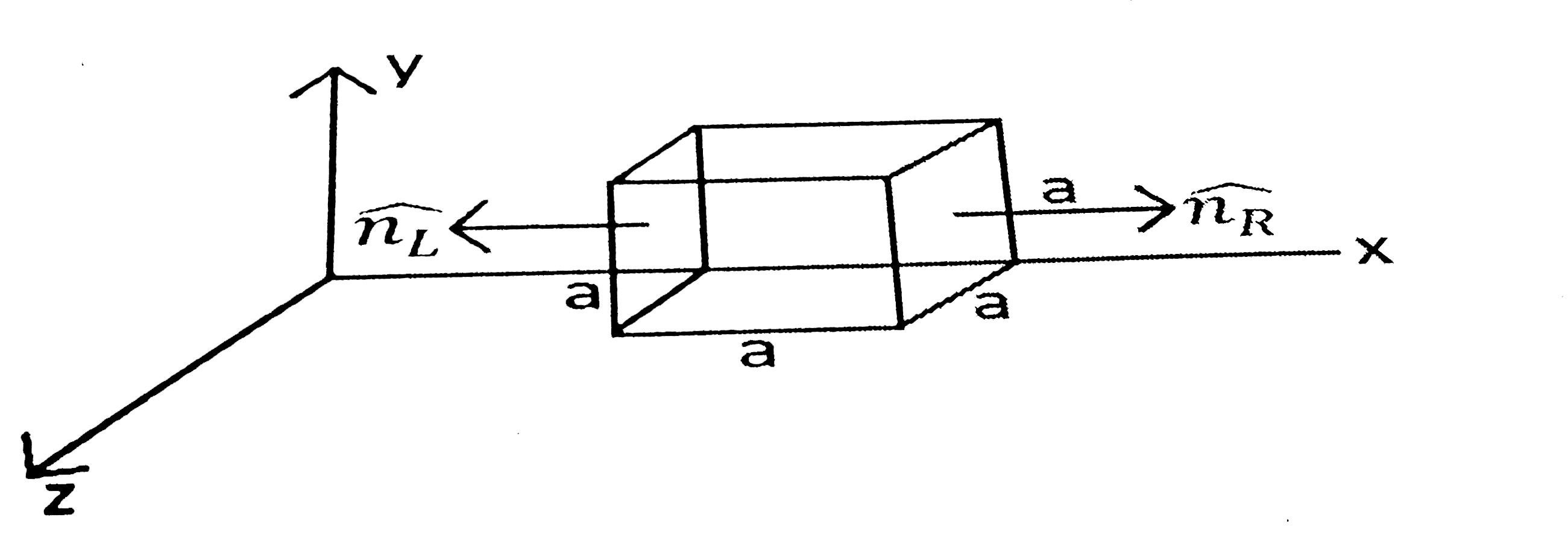
View SolutionElectric field of an electromagnetic wave →E=E0cos(ωt−kx)ˆj . The equation of corresponding magnetic field at t=0 should be
View Solution

