A smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. . A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

Let the particle displace slightly toward right at a distance
r from the centre. The force acting on the particle is
or
Hence, the force acting on the particle is making the particles
execute SHM. Comparing with we get
Hence, the time period of oscillation of the particle is
.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.2
Explore 14 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
There is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
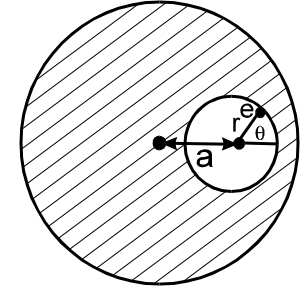
View Solution
Knowledge Check
Potential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
AρR26ε0BρR24ε0CρR23ε0DρR22ε0If a charge q is placed at the centre of imaginary sphere of radius r then the N.E.I. at a point on such a sphere is
A4πr2qBq4πr2C∈0kEDboth 'b' and 'c'A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
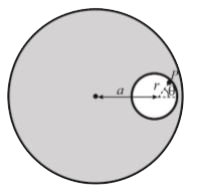 A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionRepeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View SolutionA sphere of radius R is charged uniformly with a volume charge density. It is disassembled and reassembled in two identical spheres kept far from each other.
View SolutionAn insulating solid sphere of radius R has a uniformaly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: Wgen a charge 'q' is taken from the centre to the surface of the sphere, its potential energy charges by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View Solution

