An electric field given by →E=4ˆi−(20y2+2)ˆj pierces a Gussian cube of side 1 m placed at origin such that its three sides represents x,y and z axes. The net charge enclosed within the cube is x×10−10C, where is _____. (take ∈0=8.85×10−12N−1m−2C2)
The correct Answer is:A
To solve the problem, we will use Gauss's law, which states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ε₀). The electric field given is:
→E=4^i−(20y2+2)^j
Step 1: Determine the flux through each face of the cube
The cube is placed at the origin with sides along the x, y, and z axes, and has a side length of 1 m. We will calculate the electric flux through each face of the cube.
Face 1 (ABCD): (z = 0)
- The area vector →A=dA^k
- The electric field at z = 0 is →E=4^i−(20y2+2)^j
- The flux through this face is:
ΦABCD=∫→E⋅→A=∫10∫10(4^i−(20y2+2)^j)⋅(dA^k)=0
Since the electric field is perpendicular to the area vector, the flux is zero.
Face 2 (EFGH): (z = 1)
- The area vector →A=dA(−^k)
- The electric field at z = 1 is still →E=4^i−(20y2+2)^j
- The flux through this face is:
ΦEFGH=∫→E⋅→A=0
Again, the electric field is perpendicular to the area vector, so the flux is zero.
Face 3 (ADHE): (y = 0)
- The area vector →A=dA(−^i)
- The electric field at y = 0 is →E=4^i−2^j
- The flux through this face is:
ΦADHE=∫10∫10(4^i−2^j)⋅(−dA^i)=−∫104dA=−4
Face 4 (BCGF): (y = 1)
- The area vector →A=dA^j
- The electric field at y = 1 is →E=4^i−22^j
- The flux through this face is:
ΦBCGF=∫10∫10(4^i−22^j)⋅(dA^j)=−22⋅1=−22
Face 5 (ABFE): (x = 0)
- The area vector →A=dA(−^i)
- The electric field at x = 0 is →E=4^i−2^j
- The flux through this face is:
ΦABFE=∫10∫10(4^i−2^j)⋅(−dA^i)=−∫104dA=−4
Face 6 (DCGH): (x = 1)
- The area vector →A=dA^i
- The electric field at x = 1 is →E=4^i−2^j
- The flux through this face is:
ΦDCGH=∫10∫10(4^i−2^j)⋅(dA^i)=4⋅1=4
Step 2: Calculate the total flux through the cube
Now, we sum the fluxes through all faces:
Φtotal=0+0−4−22−4+4=−26
Step 3: Use Gauss's Law to find the enclosed charge
According to Gauss's law:
Φtotal=Qenclosedϵ0
Where ϵ0=8.85×10−12N−1m−2C2.
Thus, we have:
−26=Qenclosed8.85×10−12
Qenclosed=−26×8.85×10−12=−2.31×10−10C
Step 4: Express the charge in the required format
The problem states that the charge is in the form x×10−10C. Therefore:
x=−2.31
Final Answer
The value of x is −2.31.
---
- The area vector →A=dA^k
- The electric field at z = 0 is →E=4^i−(20y2+2)^j
- The flux through this face is:
ΦABCD=∫→E⋅→A=∫10∫10(4^i−(20y2+2)^j)⋅(dA^k)=0
Since the electric field is perpendicular to the area vector, the flux is zero.
- The area vector →A=dA(−^k)
- The electric field at z = 1 is still →E=4^i−(20y2+2)^j
- The flux through this face is:
ΦEFGH=∫→E⋅→A=0
Again, the electric field is perpendicular to the area vector, so the flux is zero.
- The area vector →A=dA(−^i)
- The electric field at y = 0 is →E=4^i−2^j
- The flux through this face is:
ΦADHE=∫10∫10(4^i−2^j)⋅(−dA^i)=−∫104dA=−4
- The area vector →A=dA^j
- The electric field at y = 1 is →E=4^i−22^j
- The flux through this face is:
ΦBCGF=∫10∫10(4^i−22^j)⋅(dA^j)=−22⋅1=−22
- The area vector →A=dA(−^i)
- The electric field at x = 0 is →E=4^i−2^j
- The flux through this face is:
ΦABFE=∫10∫10(4^i−2^j)⋅(−dA^i)=−∫104dA=−4
- The area vector →A=dA^i
- The electric field at x = 1 is →E=4^i−2^j
- The flux through this face is:
ΦDCGH=∫10∫10(4^i−2^j)⋅(dA^i)=4⋅1=4
Φtotal=0+0−4−22−4+4=−26
Φtotal=Qenclosedϵ0
Where ϵ0=8.85×10−12N−1m−2C2.
−26=Qenclosed8.85×10−12
Qenclosed=−26×8.85×10−12=−2.31×10−10C
x=−2.31
Similar Questions
An electric field given by ¯¯¯E=4ˆi−(3y2+2)ˆj pierces Gaussian's cube of side 1 m placed at origin such that its three sides represents x1y and z axis. The net charge enclosed within the cube is given by −neo. Find the value of n.
'(##CEN_KSR_PHY_JEE_C18_E01_024_Q11##)'
View SolutionAn electric field given by →E=4ˆi+3(y2+2)ˆj pierces a gaussian cube of side 1m placed at origin such that one of its corners is at origin and rest of sides are along positive side of coordinate axis. Find the magnitude of net charge enclosed within the cube
[3∈0]
View Solution
Knowledge Check
An electric field given by →E=4ˆi+3(y2+2)ˆj passes through Gaussian cube of side 1m placed at origin such that its three sides represents x,y and z axis. This net charge enclosed within the cube is
A4ε0B3ε0C4ε0DzeroIn space electric field is given by →E=150y2JNC. A cube of side 0.5m is placed with one corner at origin along + y axis. Find charge enclosed inside cube:
A3.8x10−11CB16.6x10−11CC8.3x10−10CD8.3x10−11CElectric field is given by →E=(8ˆi+4ˆj+3ˆk)NC−1. Electric flux through Y-Z plane X-Z plane are in ratio
A4:3:8B8:4:3C3:8:4D3:4:8
An electric field is given by →E=4ˆi+3(y2+2)ˆj pierces gaussian cube of side 1 m placed at origin such that one of its corners is at origin & rest of sides are along positive side of coordinate axis. If the magnitude of net charge enclosed is n ɛ0 then n (in SI units) will be equal to
View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. The charge enclosed in the cube of side 1m oriented as shown in the diagram is given by α∈0. Find the value of α.
View SolutionAn electric field →E=(10ˆi+20ˆj)N/C exists in the space. If the potential at the origin is taken to be zero, find the potential at (3m, 3m).
View SolutionIf electric field is
(a) →E=2axyˆi+a(x2−y2)ˆj
(b) →E=ayˆi+(ax+bz)ˆj+byˆk)
Find potential.
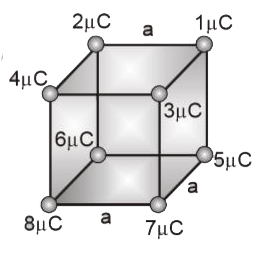
View SolutionThe total flux associated with given cube will be - where 'a' is side of cube :-
(1∈0=4π×9×109)
View Solution

