A non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density ρ=kr2 where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre?
Step by step video & image solution for A non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density rho=kr^(2) where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.2
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.3
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.1
Explore 1 Video
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:Advance MCQs
Explore 33 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
Similar Questions
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b, where r is distance from the center of the ball, a and b are constants. Calculate the charge density inside the ball.
View SolutionA ball of radius R has a uniformly distributed charge Q. The surrounding space of the ball is filled with a volume charge density ρ=br , where b is a constant and r is the distance from the centre of the ball. It was found that the magnitude of electric field outside the ball is independent of distance r. (a) Find the value of Q. (b) Find the magnitude of electric field outside the ball.
View Solution
Knowledge Check
A solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
A1/x2B1/xCx3Dx2The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
A(a) −6aε0rB(b) −24πaε0C(c) −6aε0D(d) −24πaε0rThe electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
A−24πaε0rB−6πε0rC−24πaε0D−6aε0
A solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View SolutionA system consits of a ball of radus R carrying spherically symmetric charge and the surrounding space filled with a charge of volume density ρ=α/r , wehre α is a constant, r is the distance from the centre of the ball. Find the ball's the charge at whcih the magnitude of the electric field strength vector is independent of r outside the ball. How high is this strength ? The permittives of the ball and the surrounding space are assumed to be equal to unity.
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
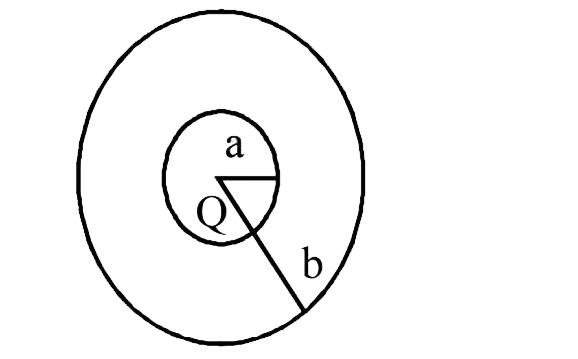
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View Solution

