Question

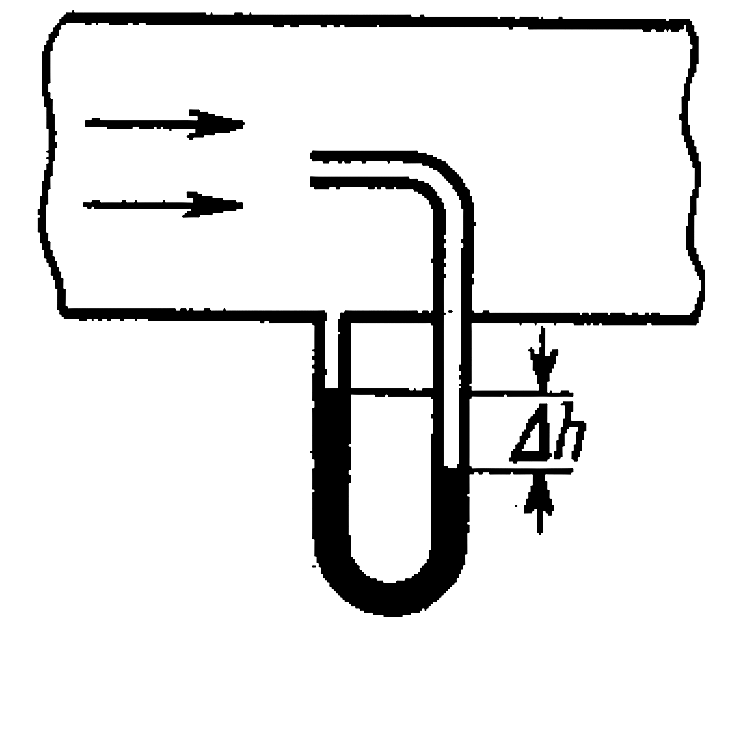
Two manometric tubes are mounted on a horizontal pipe of varying cross-section at the section $S_1$ and $S_2$ (figure). Find the volume of water flowing across the pipe's section per unit time if the difference in water columns is equal to $\Delta h$.

Explanation

From the conservation of mass
`v_1S_1=v_2S_2` (1)
But `S_1 lt S_2` as shown in the figure of the problem, therefore
`v_1 gt v_2`
As every streamline is horizontal between 1 & 2, Bernoull's theorem becomes
`p+1/2rhov^2=const ant`, which gives
`p_1 lt p_2` as `v_1 gt v_2`
As the difference in height of the water column is `Deltah`, therefore
`p_2-p_1=rhogDeltah` (2)
From Bernoull's theorem between points 1 and 2 a streamline
`p_1+1/2rhov_1^2=p_2+1/2rhov_2^2`
or, `p_2-p_1=1/2rho(v_1^2-v_2^2)`
or `rhogDeltah=1/2rho(v_1^2-v_2^2)` (3) (using Eq. 2)
using (1) in (3), we get
`v_1=S_2sqrt((2gDeltah)/(S_2^2-S_1^2))`
Hence the sought volume of water flowing per see
`Q=v_1S_1=S_1S_2sqrt((2gDeltah)/(S_2^2-S_1^2))`