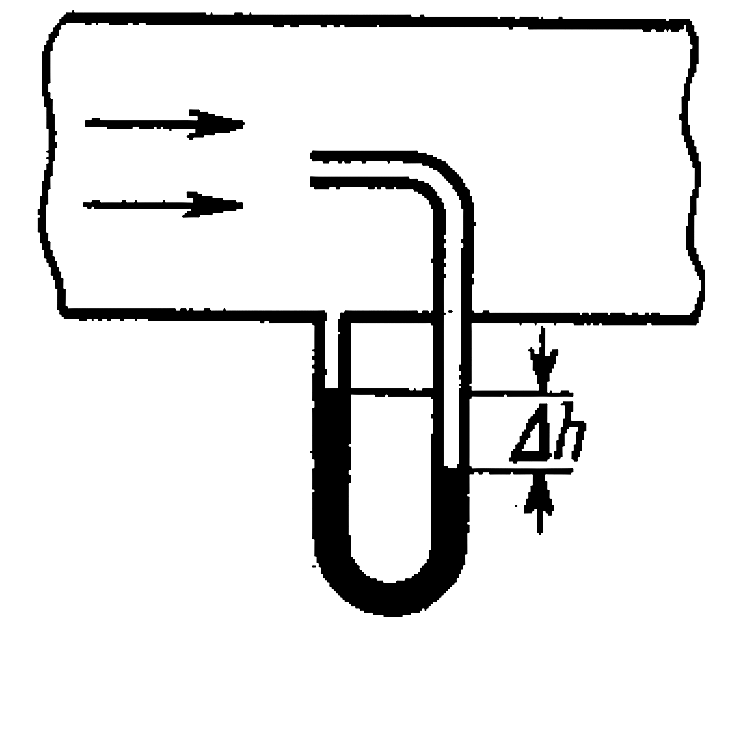
A piot tube figure is mounted along the axis of a gas pipeline whose cross -sectional area is equal to S.

Assuming the viscosity to be negligible, find the volume of the gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquids and the gas are ρ0 and ρ respectively.
Step by step video & image solution for A piot tube figure is mounted along the axis of a gas pipeline whose cross -sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of the gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Deltah, and the densities of the liquids and the gas are rho_(0) and rho respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:practice Exercise 7.1
Explore 10 Videos
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:Practice Exercise 7.2
Explore 8 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Unsolved Numerical
Explore 94 Videos
Similar Questions
A Pitot tube (figure) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquid and the gas are ρ0 and ρ respectively.
View SolutionTwo manometric tubes are mounted on a horizontal pipe of varying cross-section at the section S1 and S2 (figure). Find the volume of water flowing across the pipe's section per unit time if the difference in water columns is equal to Δh.

View Solution
Knowledge Check
In streamline flow of liquid through a pipe of uniform cross sectional area, all stremlines are
Adivided into plane layers.Bdivided into reactangular blocks.Cparallel to the axis of the tube.Dcircular in shape.If cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
 A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of these
A√2g(x−y)BA1A2√2g(x−y)CA2A1√2g(x−y)DNone of theseA liquid is under stream lined motion through a horizontal pipe of non uniform cross section. If the volume rate of flow at cross section a is V, the volume rate of flow at cross section a2 is
AV2B2VCV4DV
A tube of length l and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The fluid flow velocity depends on the distance r from the axis of the tube as v=v0(1−r2/R2). Find:
(a) the volume of the fluid flowing across the section of the tube per unit time:
(b) the kinetic energy of the fluid within the tube's volume,
(c) the friction force exerted on the tube by the fluid,
(d) the pressure difference at the ends of the tube.
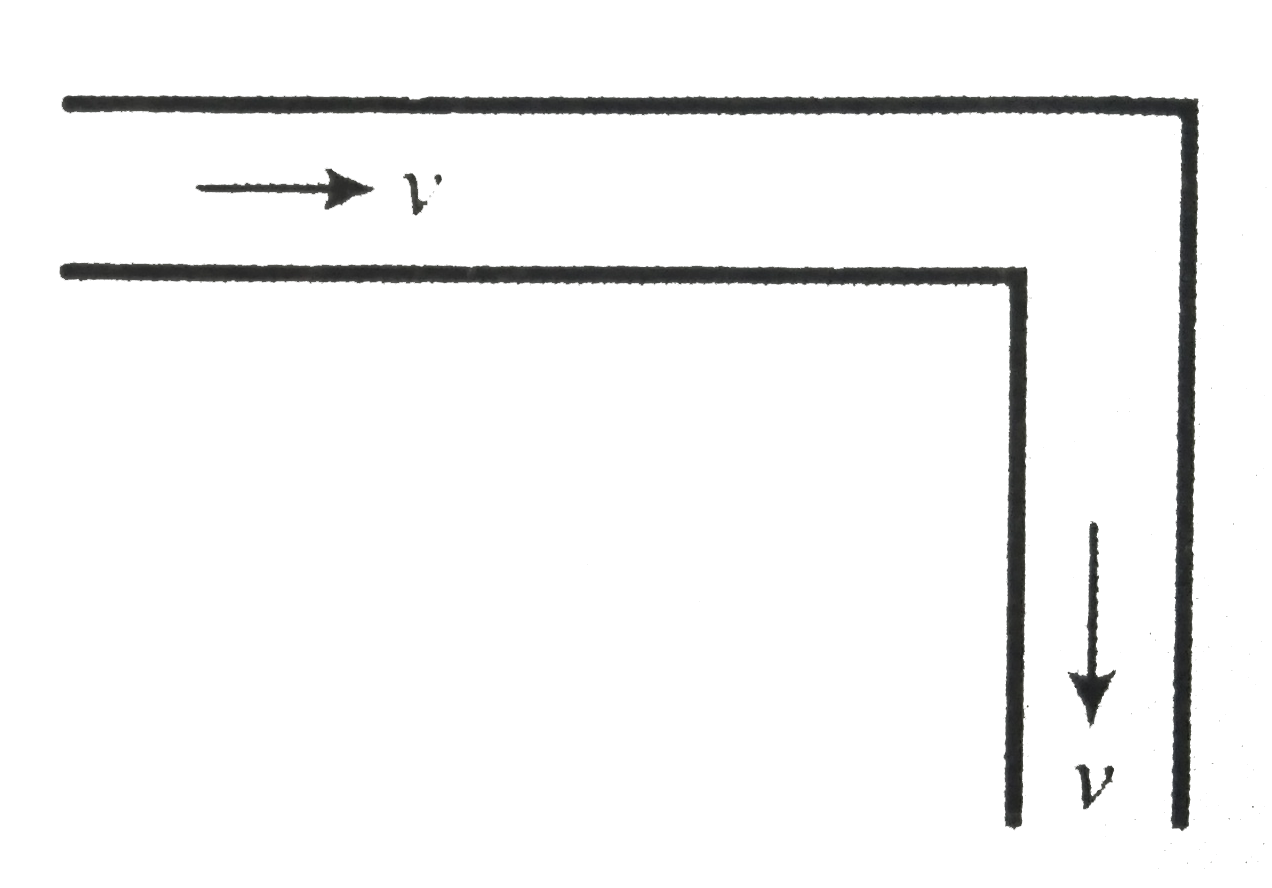
View SolutionA liquid of density ρ is flowing inside a pipe of cross - sectional area A. The pipe is bent in the shape of a right angle as shown. What force should be exerted on the pipe at the corner to keep it fixed in the two cases shown?

View SolutionIn the figure shown density of lower liquid is three times of density of upper liquid. The cross- sectional areas of openings shown are same. The ratio of mass flow rate from upper opening to lower opening at initial moment is:
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
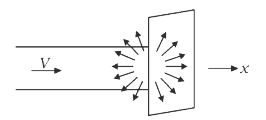
View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View Solution

