At what distance from the center of the earth will a 1 kg object have a weight of 1N ? If released from rest at this distance, What will its initial acceleration be ?
The correct Answer is:2.023×107m
To solve the problem, we need to determine the distance from the center of the Earth where a 1 kg object will have a weight of 1 N, and then find its initial acceleration if released from rest at that distance.
1. Understanding Weight and Gravitational Acceleration:
The weight W of an object is given by the formula:
W=m⋅g
where m is the mass of the object and g is the gravitational acceleration. For our case, we have:
W=1N,m=1kg
Therefore, we can write:
1N=1kg⋅g
From this, we find:
g=1m/s2
2. Using the Formula for Gravitational Acceleration:
The gravitational acceleration at a distance r from the center of the Earth can be expressed as:
g=G⋅Mr2
where G is the universal gravitational constant, and M is the mass of the Earth.
3. Relating Gravitational Acceleration at the Surface of the Earth:
The gravitational acceleration at the surface of the Earth g0 is given by:
g0=G⋅MR2
where R is the radius of the Earth.
4. Setting Up the Equation:
We know that at the distance r where the weight is 1 N:
G⋅Mr2=1m/s2
We can relate this to the surface gravity:
G⋅Mr2=G⋅MR2⋅R2r2
Simplifying gives:
g0r2=1
Thus:
r2=10⋅R2
5. Calculating the Distance r:
Taking the square root of both sides, we find:
r=√10⋅R
Given that the radius of the Earth R≈6400×103m:
r=√10⋅(6400×103)≈2.203×107m
6. Finding Initial Acceleration:
The initial acceleration a when the object is released from rest can be calculated using the gravitational acceleration at that distance:
a=g=1m/s2
Final Answers:
- The distance from the center of the Earth where the weight of the object is 1 N is approximately 2.203×107m.
- The initial acceleration of the object when released from rest at this distance is 1m/s2.
The weight W of an object is given by the formula:
W=m⋅g
where m is the mass of the object and g is the gravitational acceleration. For our case, we have:
W=1N,m=1kg
Therefore, we can write:
1N=1kg⋅g
From this, we find:
g=1m/s2
The gravitational acceleration at a distance r from the center of the Earth can be expressed as:
g=G⋅Mr2
where G is the universal gravitational constant, and M is the mass of the Earth.
The gravitational acceleration at the surface of the Earth g0 is given by:
g0=G⋅MR2
where R is the radius of the Earth.
We know that at the distance r where the weight is 1 N:
G⋅Mr2=1m/s2
We can relate this to the surface gravity:
G⋅Mr2=G⋅MR2⋅R2r2
Simplifying gives:
g0r2=1
Thus:
r2=10⋅R2
Taking the square root of both sides, we find:
r=√10⋅R
Given that the radius of the Earth R≈6400×103m:
r=√10⋅(6400×103)≈2.203×107m
The initial acceleration a when the object is released from rest can be calculated using the gravitational acceleration at that distance:
a=g=1m/s2
- The distance from the center of the Earth where the weight of the object is 1 N is approximately 2.203×107m.
- The initial acceleration of the object when released from rest at this distance is 1m/s2.
Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Advance MCQs
17 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
A positive point charge is released from rest at a distance r0 from a positive line charge with uniform density. The speed (v) of the point charge, as a function of instantaneous distance r from line charge, is proportional to:

View SolutionSuppose you are standing on a tall ladder. If your distance from the centre of the earth is 2 R, what will be your weight ?
View Solution
Knowledge Check
The distance from center of circle to its boundary is known as
ADiameterBRadiusCCircumferenceDChordAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
A2RBRC1.414RD0.414RThe gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
AUBUrCUrDU2r
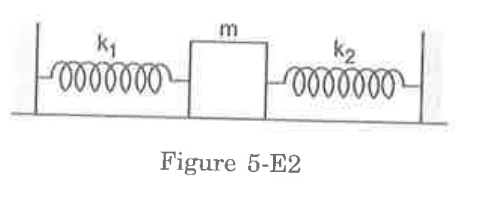
Both the springs shown in figure are untretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
View SolutionAn object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy ?
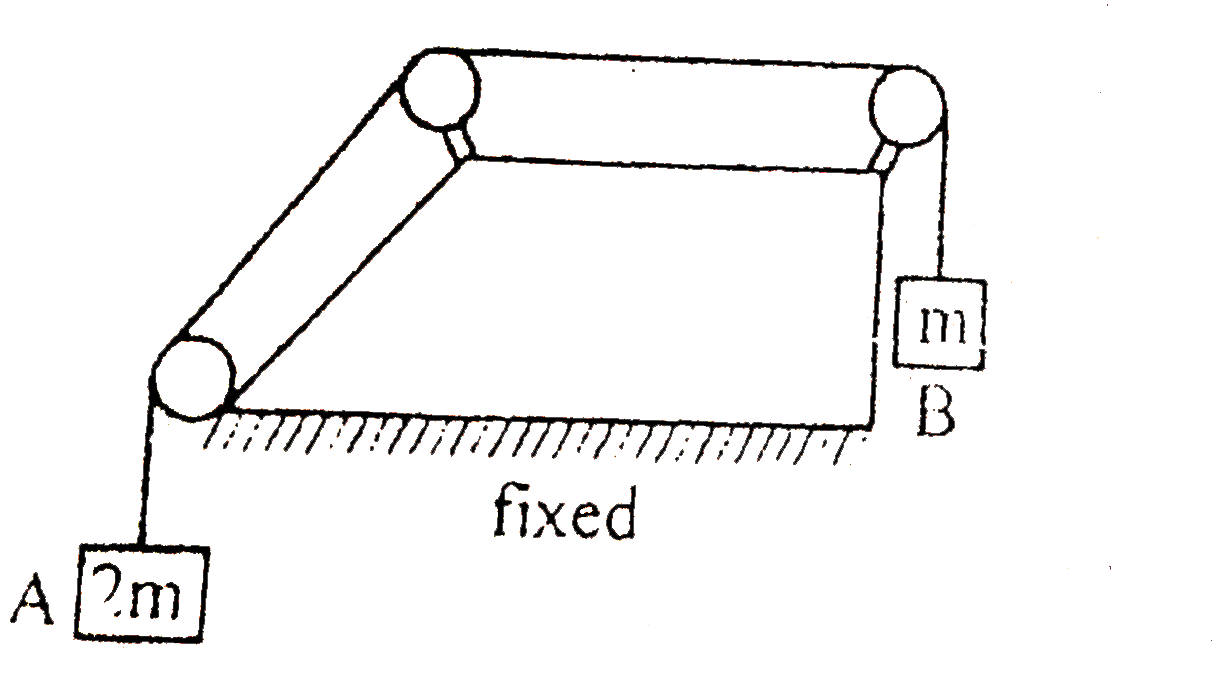
View SolutionWhat is the acceleration of block A when the system is released from rest ?
View SolutionThe weight of a body a distance 2R from the centre of the earth of radius 'R' is 2.5 N. If the distance is 3R from the centre of the earth the weight of the body will be
View SolutionA particle of mass 0.3kg is subjected to a force F=kx with k=15N/m and x being its distance from the origin. What will be its initial acceleration if it is released from a point 20cm away from the origin.
View Solution
