A solid copper cylinder of length $l = 65 c m$ is placed on a horizontal surface and subjected to a vertical compressive force $F = 1000 N$ directed downward and distributed uniformly over the end face. What will be the resulting change of the volume of the cylinder in cubic millimeters?

Video Solution

Text Solution

Verified by Experts

Volume of a solid cylinder
$V = π r^{2} l$
So, $\frac{Δ V}{V} = \frac{π 2 r Δ r l}{π r^{2} l} + \frac{π r^{2} Δ l}{π r^{2} l} = \frac{2 Δ r}{r} + \frac{Δ l}{l}$ (1)
But longitudinal strain $Δ l / l$ and accompanying lateral strain $Δ r / r$ are related as
$\frac{Δ r}{r} = - μ \frac{Δ l}{l}$ (2)
Using (2) in (1), we get:
$\frac{Δ V}{V} = \frac{Δ l}{l} (1 - 2 μ)$ (3)
But $\frac{Δ l}{l} = \frac{- F / π r^{2}}{E}$
(Because the increment in the length of cylinder $Δ l$ is negative)
So, $\frac{Δ V}{V} = \frac{- F}{π r^{2} E} (1 - 2 μ)$
Thus, $Δ V = \frac{- F l}{E} (1 - 2 μ)$
Negative sign means that the volume of the cylinder has decreased.

Updated on:21/07/2023

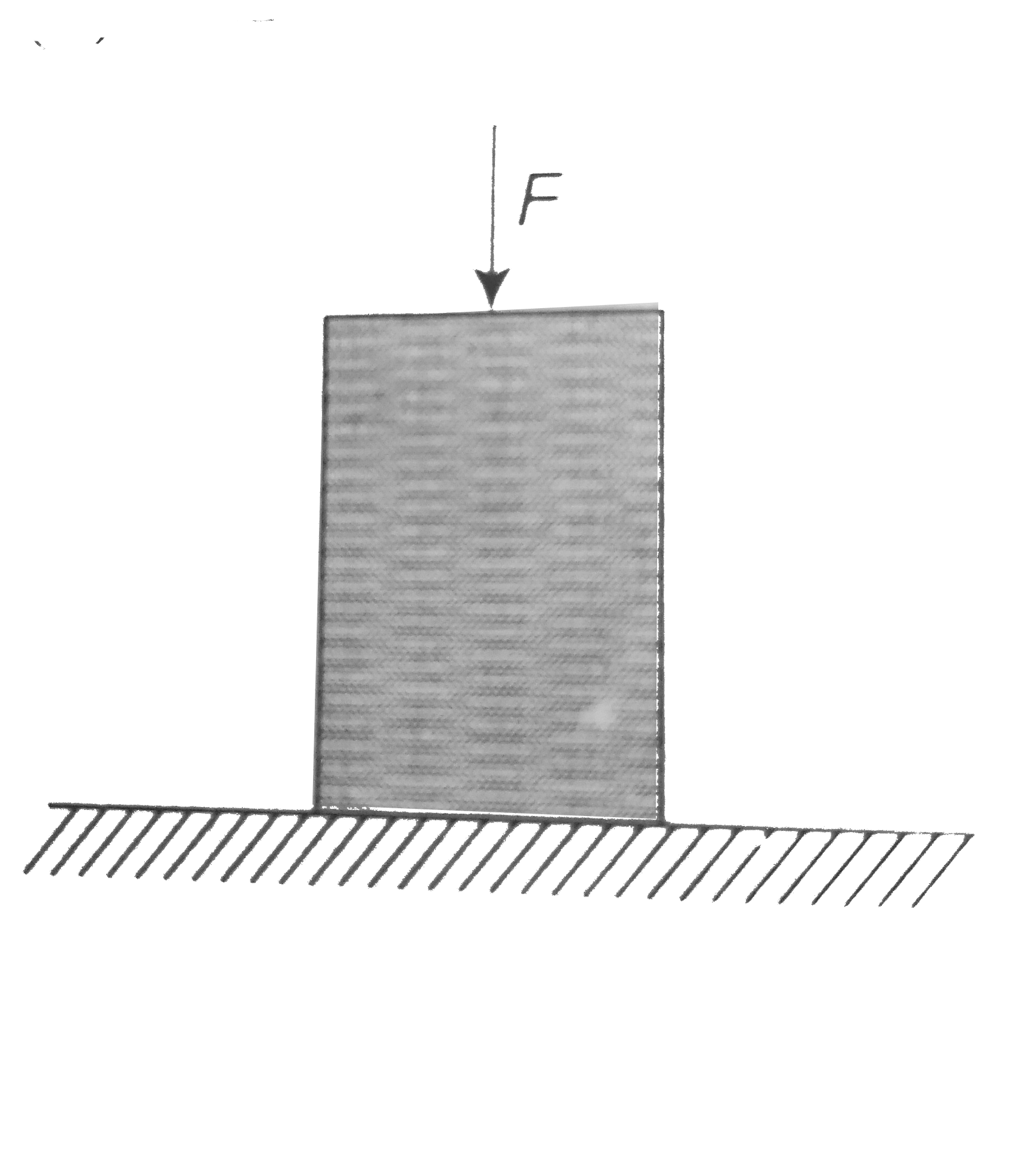
A metal cylinder of length $L$ is subjected to a uniform compressive to a uniform compressive force $F$ as shown in the figure. The material of the cylinder has Young's modulus $Y$ and poisson's ratio $σ$ The change in volume of the cylinder is
A $\frac{σ F L}{Y}$
B $\frac{(1 - σ) F L}{Y}$
C $\frac{(1 + 2 σ) F L}{Y}$
D $\frac{(1 - 2 σ) F L}{Y}$
A uniform rod of mass $m$ and length $l$ is placed over a smooth horizontal surface along the $y$ -axis and is at rest as shown in Fig. An impulsive force $F$ is applied for a small time $△ t$ along $x$ -direction at point $A$ . The $x$ -coordinate of end $A$ of the rod when the rod becomes parallel to $x$ -axis for the first time is [initially, the coordinate of centre of mass of the rod is $(0, 0)$ ]

A $\frac{π l}{12}$
B $\frac{l}{2} (1 + \frac{π}{12})$
C $\frac{1}{2} (1 - \frac{π}{6})$
D $\frac{l}{2} (1 + \frac{π}{6})$
A uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time $Δ t$ along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).

A $\frac{π l}{12}$
B $\frac{l}{2} (1 + \frac{π}{12})$
C $\frac{l}{2} (1 - \frac{π}{6})$
D $\frac{l}{2} (1 + \frac{π}{6})$