
A uniform elastic rod of cross section area A natural length L and Young's modulus Y is placed on a smooth horizontal surface. Now two horizontal forces (of magnitude F and 3F) directed along the length of rod and in opposite direction act at two of its ends as shown . After the rod has acquired steady state, the extension of the rod will be
2FYAL
4FYAL
FYAL
3F2YAL
The correct Answer is:A
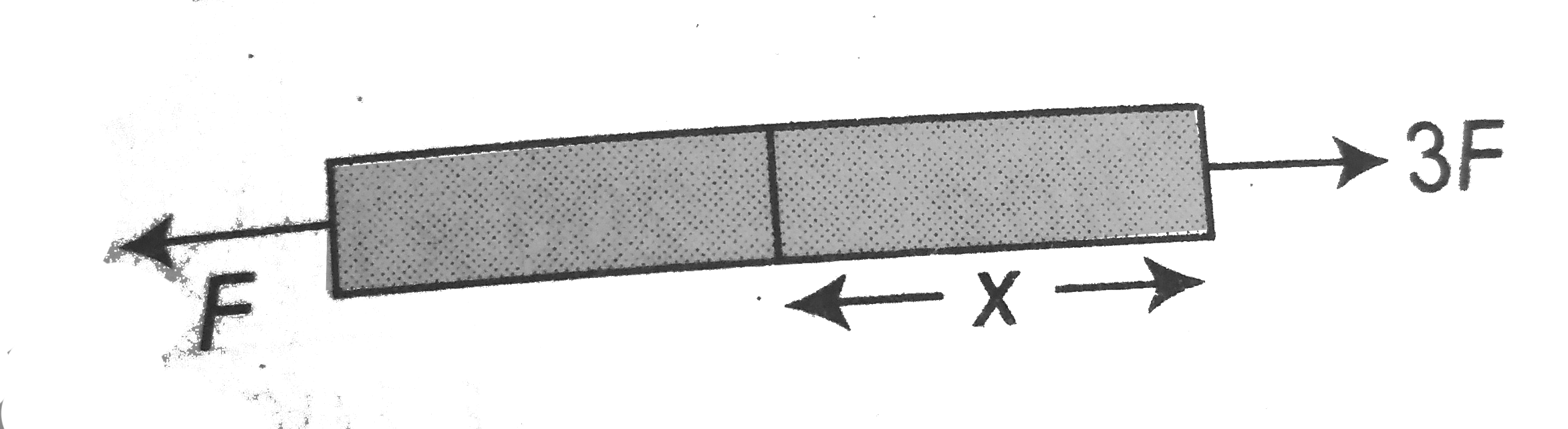
Tension in rod at a distance x from right edge is
T=F(3−2xL)
Net extension in rod =∫L0T4Adx=2FYAL
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus
29 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Elasticity And Work Done In Stretching A Wire
25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
A smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionA straight rod AB of mass M and length L is placed on a frictionless horizontal surface. A horizontal force having contstant magnitude F and fixed direction starts acting at the end A. The rod is initially perpendicular to the force. Find the initial acceleration of end B.
View Solution
Knowledge Check
A uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
 A2FL5AYB3FL5AYC3FL8AYD8FL3AY
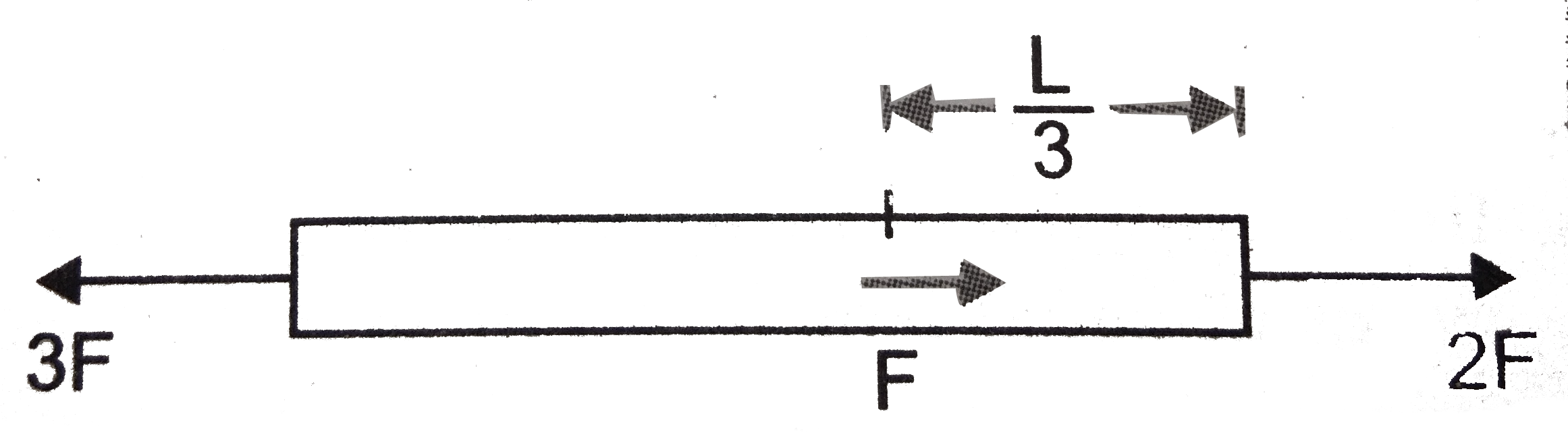
A2FL5AYB3FL5AYC3FL8AYD8FL3AYA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elongation in section PQ of rod and section QR of rod isA1:1B3:5C5:7D1:2A uniform plank of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
AF/AYB2F/AYC12(F/AY)D3F/AY
A thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Ratio of elastic potential energy stored in section PQ and section QR of the rod is
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA smooth uniform string of natural length L0, cross-sectional area A and Young's modulus Y is pulled along its length by a force F on a horizontal smooth surface. The elastic potential energy stored in the string is
View Solution
