A uniform elastic plank moves due to a constant force F0 applied at one end whose area is S. The Young's modulus of the plank is Y. The strain produced in the direction of force is
Let us consider an element of the rod at a distance x from the free end (figure). For the considered element 'T−T' are internal restoring forces which produce elongation and dT provides the acceleration to the element. For the element from Newton's law:
dT=(dm)w=(mldx)Fom=Foldx
As free end has zero tension, on integrating the above expression,
T∫odT=F0lx∫odx or T=Folx
Elongation in the considered element of length dx :
δξ=σE(x)dx=TSEdx=FxoxdxSEL
Thus total elongation ξ=FoSEll∫xdx=Fol2SE
Hence the sought strain
σ=ξl=Fo2SE

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
There is a uniform elastic plank moveing over a smooth horizontal plane due to a constant force F0 distributed uniformly over the front end of the plank whose area is A. If Young's modulus of the material is Y, then the compressive strain of the plank along the direction of the force is F0KAY. What is K = ?
View SolutionA car moves with a constant speed toward East. A force is applied on the car to make it stop. The direction of the applied force is toward
View Solution
Knowledge Check
A uniform plank of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
AF/AYB2F/AYC12(F/AY)D3F/AYWhen a constant force is applied to a body, it moves with unifrom
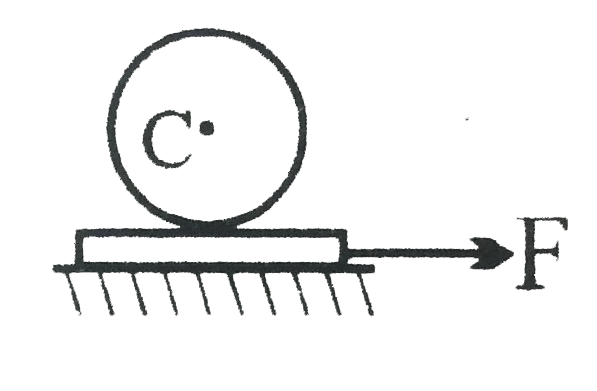
AspeedBvelocityCaccelerationDmomentumIn the following problems, indicate the correct direction of friction force acting on the cylinder, which is pulled on a rough surface by a constant force F.
A cylinder is placed on a rough plank which in turn is placed on a smooth surface. The plank is pulled with a constant force F. The friction force can be given by which of the following diagrams.
 .A
.A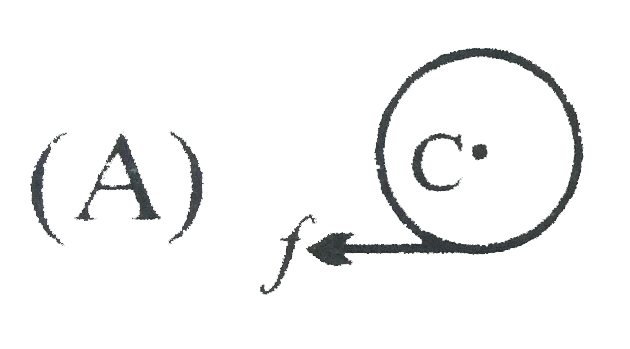 B
B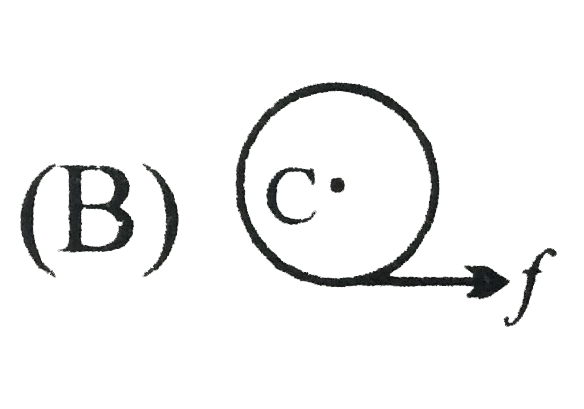 C
C Dcannot be interpreted
Dcannot be interpreted
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA plank of mass m1 with a uniform solid sphere of mass m2 placed on it rests and a force F is applied to the plank. The acceleration of the plank provided there is no sliding between the plank and the sphere is (Fm1+n7m2) then the value of n is

View SolutionA plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA steel rope has length L area of cross-section A young's modulus Y [density =d] (i) it is pulled on a horizotnal fritionless floor with a constant horizontal force F=|dALg|/2 applied at one end find the strain at the midpoint.
(ii). If the steel rope is vertical and moving with the force acting vertically up at the upper end find the strain at distance L/3 from lowerr end.
View SolutionWhen a force is applied at one end of an elastic wire, it produce a strain E in the wire. If Y is the Young's modulus of the material of the wire, the amount of energy stored per unit volume of the wire is given by
View Solution