A conducting cylinder of length L is placed on a rough horizontal floor. A horizontal magnetic field is applied perpendicular to the length of cylinder. F1 and F2 are the minimum forces required to move the cylinder for two possible directions of current, which can be passed through the cylinder. Calculate the coefficient of friction between the floor and the cylinder. Assume F1>F2.
To solve the problem, we will analyze the forces acting on the conducting cylinder in both cases of current direction and derive the expression for the coefficient of friction.
1. Understanding the Setup:
- We have a conducting cylinder of length L placed on a rough horizontal floor.
- A horizontal magnetic field B is applied perpendicular to the length of the cylinder.
- The forces F1 and F2 are the minimum forces required to move the cylinder for two possible directions of current.
2. Case 1: Current in the Upward Direction:
- When the current I flows upward, the magnetic force F1 acting on the cylinder can be calculated using the formula:
F1=I⋅L⋅B
- The normal force N1 acting on the cylinder is given by:
N1=mg+F1=mg+I⋅L⋅B
- The frictional force Ffriction1 that opposes the motion is:
Ffriction1=μN1=μ(mg+I⋅L⋅B)
3. Case 2: Current in the Downward Direction:
- When the current I flows downward, the magnetic force F2 acting on the cylinder is:
F2=I⋅L⋅B
- The normal force N2 in this case is:
N2=mg−F2=mg−I⋅L⋅B
- The frictional force Ffriction2 is:
Ffriction2=μN2=μ(mg−I⋅L⋅B)
4. Setting Up the Equations:
- For the cylinder to start moving in either case, the applied force must equal the frictional force.
- Therefore, we have:
F1=μ(mg+I⋅L⋅B)(1)
F2=μ(mg−I⋅L⋅B)(2)
5. Solving for mg:
- From equation (1):
mg=F1μ−I⋅L⋅B(3)
- From equation (2):
mg=F2μ+I⋅L⋅B(4)
6. Equating Equations (3) and (4):
- Setting the right-hand sides of equations (3) and (4) equal gives:
F1μ−I⋅L⋅B=F2μ+I⋅L⋅B
7. Rearranging the Equation:
- Rearranging the equation leads to:
F1−F2μ=2I⋅L⋅B
- Therefore, we can express μ as:
μ=F1−F22I⋅L⋅B
Final Result:
The coefficient of friction μ between the floor and the cylinder is given by:
μ=F1−F22I⋅L⋅B
- We have a conducting cylinder of length L placed on a rough horizontal floor.
- A horizontal magnetic field B is applied perpendicular to the length of the cylinder.
- The forces F1 and F2 are the minimum forces required to move the cylinder for two possible directions of current.
- When the current I flows upward, the magnetic force F1 acting on the cylinder can be calculated using the formula:
F1=I⋅L⋅B
- The normal force N1 acting on the cylinder is given by:
N1=mg+F1=mg+I⋅L⋅B
- The frictional force Ffriction1 that opposes the motion is:
Ffriction1=μN1=μ(mg+I⋅L⋅B)
- When the current I flows downward, the magnetic force F2 acting on the cylinder is:
F2=I⋅L⋅B
- The normal force N2 in this case is:
N2=mg−F2=mg−I⋅L⋅B
- The frictional force Ffriction2 is:
Ffriction2=μN2=μ(mg−I⋅L⋅B)
- For the cylinder to start moving in either case, the applied force must equal the frictional force.
- Therefore, we have:
F1=μ(mg+I⋅L⋅B)(1)
F2=μ(mg−I⋅L⋅B)(2)
- From equation (1):
mg=F1μ−I⋅L⋅B(3)
- From equation (2):
mg=F2μ+I⋅L⋅B(4)
- Setting the right-hand sides of equations (3) and (4) equal gives:
F1μ−I⋅L⋅B=F2μ+I⋅L⋅B
- Rearranging the equation leads to:
F1−F2μ=2I⋅L⋅B
- Therefore, we can express μ as:
μ=F1−F22I⋅L⋅B
The coefficient of friction μ between the floor and the cylinder is given by:
μ=F1−F22I⋅L⋅B
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Very Short Answer Questions )
59 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Additional Questions )
16 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) (Short Answer Type Questions )
6 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A conducting wire of length l is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current I is established in the rod are observed to be F1 and F2(<F1) for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.

View Solution
Knowledge Check

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3mA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 NConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P? It is assumed that the cylinder does not slip.
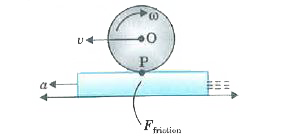 AMgBMaCMa2DMa3
AMgBMaCMa2DMa3
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
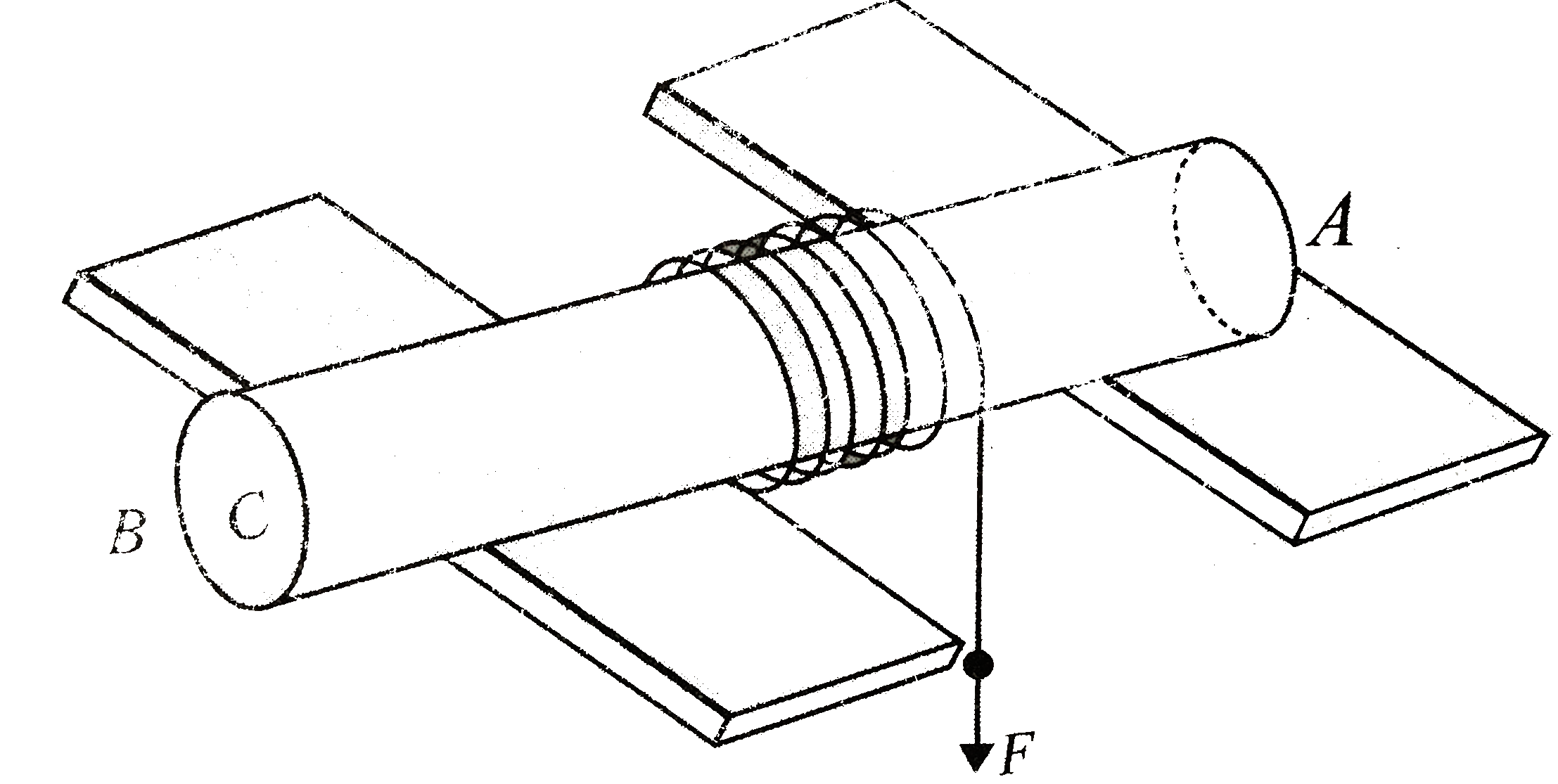
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
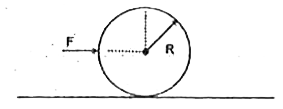
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View Solution
