A small disc A slides down with initial velocity equal to zero from the top of a smooth hill of height H having a horizontal portion. What must be the height of the horizontal portion h to ensure the maximum distance s covered by the disc? What is it equal to?
Velocity of the body at height h, vh=√2g(H−h), horizontally (from the figure given in the problem). Time taken in falling through the distance h.
t=√2hg (as initial vertical component of the velocity is zero.)
Now s=vht=√2g(H+h)×√2hg=√4(Hh−h2)
For smax, dds(Hh−h2)=0, which yields h=H2
Putting this value of h in the expression obtained for s, we get,
smax=H
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A ball is thrown with velocity 40m/s at angle 30∘ with horizontal from the top of a tower of height 60m. At what horizontal distance from the foot of tower, the ball will strike the gorund ?
View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
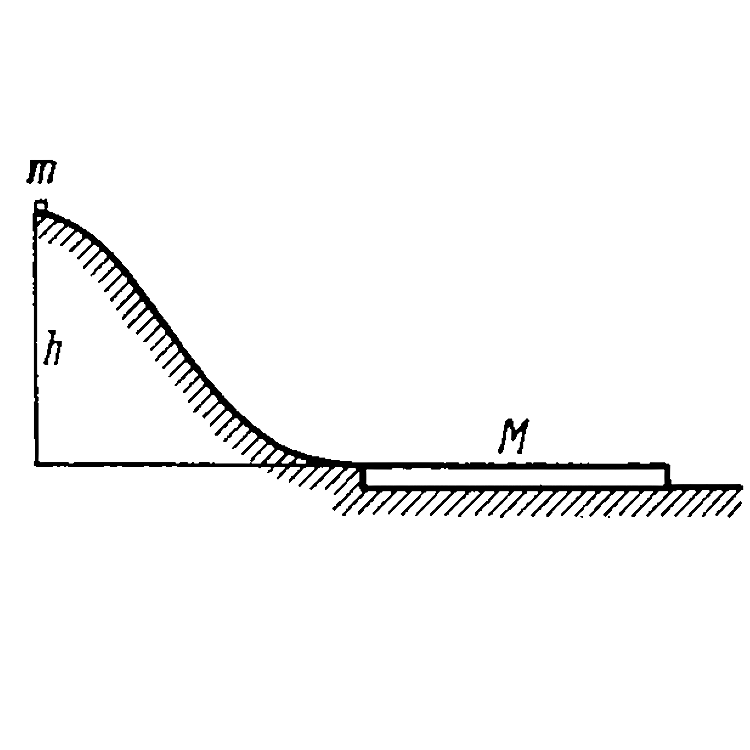
View Solution
Knowledge Check
The angle of elevation of the top of a tower at a horizontal distance equal to the height of the tower from the base of the tower is
A30∘B45∘C60∘Dany acute angleA ball is thrown from a point in level with velocity u and at a horizontal distance r from the top of a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ?
Aucosθg{(u2sin2θ+gh)1/2−usinθ}Bucosθg{(u2cos2θ+2gh)1/2−ucosθ}Cucosθg{(u2cos2θ+gh)1/2−ucosθ}Ducosθg{(u2cos2θ+gh)1/2−ucosθ}The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation P and q respectively. What is the height of the hill ?
Ahcotqcotq−cotpBhcotpcotP−cotqC2htanptanp−tanqD2htanqtanq−tanp
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
View SolutionFrom the top of a building of height h, a tower standing on the ground is observed to make an angle θ. If the horizontal distance between the building and the tower is h, the height of the tower is
View SolutionAt what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
View SolutionA particle is thrown with the velocity v with the angle α from the horizontal plane and its range on the horizontal plane is twice to the maximum height gained. Thentanα is equal to
View SolutionA particle is thrown with the velocity v with the angle α from the horizontal plane and its range on the horizontal plane is twice to the maximum height gained. Thentanα is equal to
View Solution