In the arrangement shown in figure the mass of body 1 is η=4.0 times as great as that of body 2. The height h=20cm. The masses of the pulleys and the threads, as well as the friction, are negligible. At a certain moment body 2 is released and the arrangement set in motion. What is the maximum height that body 2 will go up to?
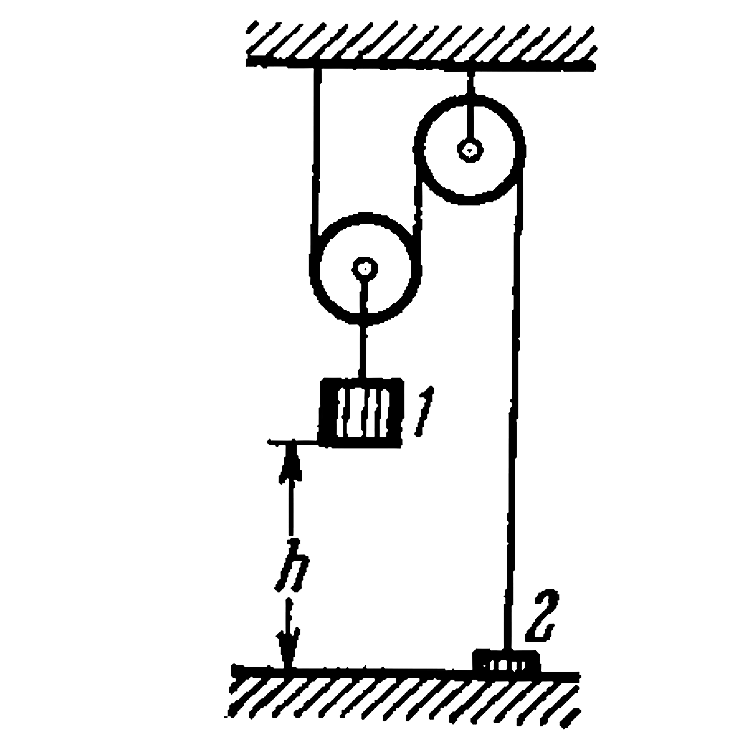
Using Newton's second law in projection form along x-axis for the body 1 and along negative x-axis for the body 2 respectively, we get
m1g−T1=m1w1 (1)
T2−m2g=m2w2 (2)
For the pulley lowering in downward direction from Newton's law along x axis,
T1−2T2=0 (as pulley is mass less)
or, T1=2T2 (3)
As the length of the thread is constant so,
w2=2w1 (4)
The simultaneous solution of above equations yields,
w2=2(m1−2m2)g4m2+m1=2(η−2)η+4 (as m1m2=η) (5)
Obviously during the time interval in which the body 1 comes to the horizontal floor covering the distance h, the body 2 moves upward the distance 2h. At the moment when the body 2 is at the height 2h from the floor its velocity is given by the expression:
v22=2w2(2h)=2[2(η−2)gη+4]2h=8h(η−2)gη+4
After the body m1 touches the floor the thread becomes slack or the tension in the thread zero, thus as a result body 2 is only under gravity for it's subsequent motion.
Owing to the velocity v2 at that moment or at the height 2h from the floor, the body 2 further goes up under gravity by the distance,
h′=v222g=4h(η−2)η+4
Thus the sought maximum height attained by the body 2:
H=2h+h′=2h+4h(η−2)(η+4)=6ηhη+4

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
In the arrangement shown in fig the mass of the ball 1 is η=1.8 times as great as that of rod 2 The length of the later is l=100 cm The masses of the pulleys and the threads as well as the friction are negligible The ball is set on the same level as the lower end of the rod and then released How soon will the ball be opposite to the other end of the rod

View SolutionIn the arrangement shown in figure the mass of the ball is η times as that of the rod. The length of the rod is L the masses of the pulleys and the threats as well as the friction, are negligible. The ball is set on the same level as the lower and of the rod and then released. How soon will the ball be opposite the upper and of the rod?

View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

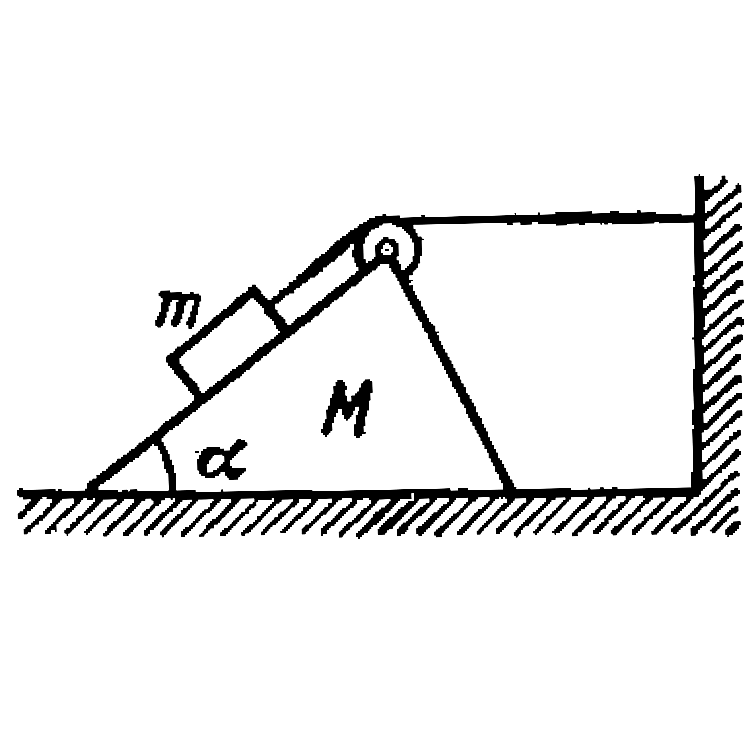
View SolutionIn the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
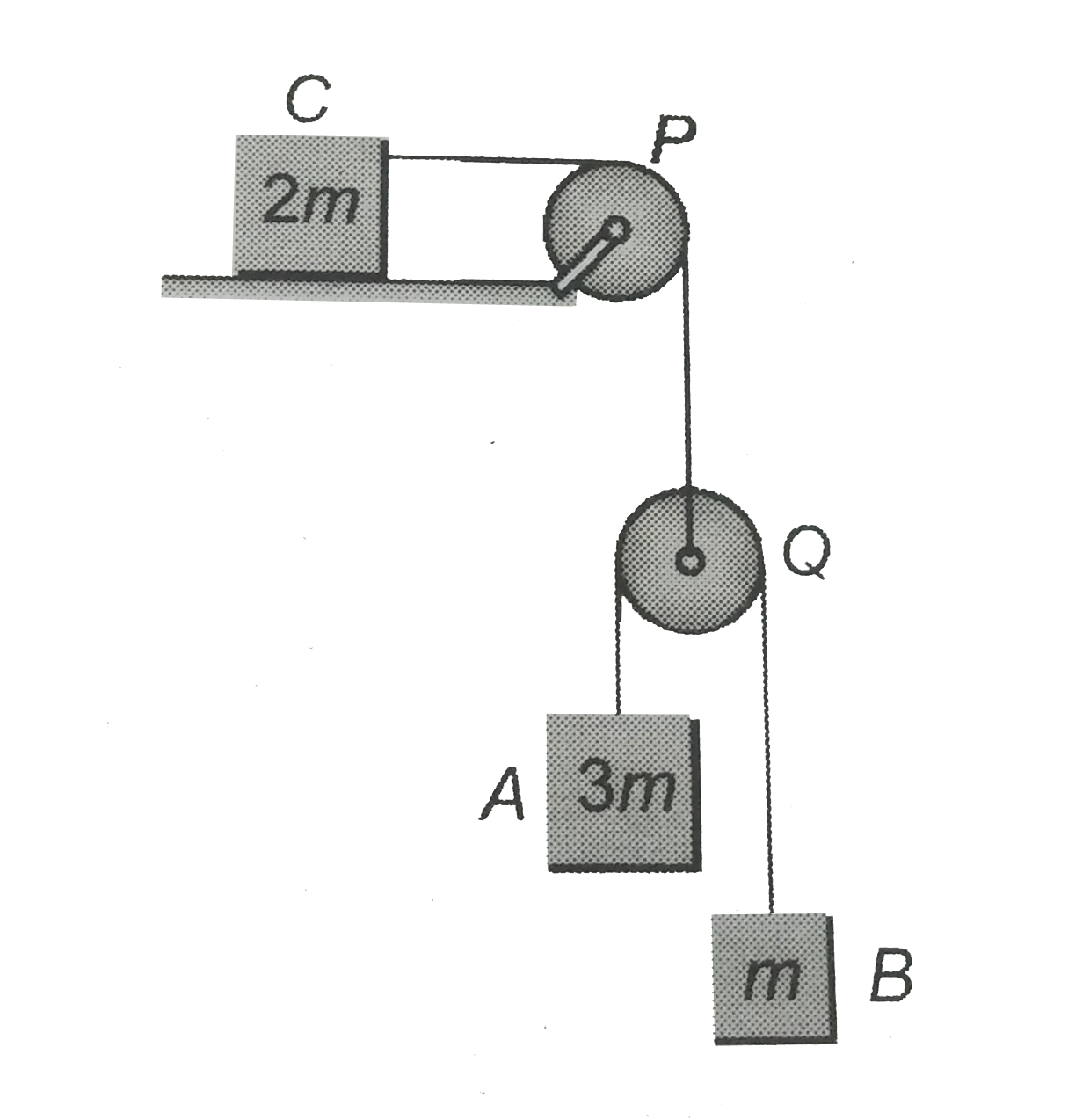
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
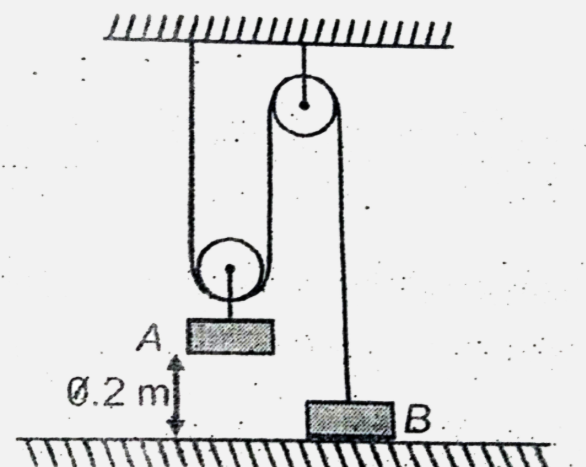
View SolutionIn the arrangement shown in figure , the mass of the body A is 4 m and that of body B is m . The height h=0⋅2 m . If the body B is released , then till what maximum height the body B will go up ? (g = 10m/s2)
View SolutionIn the arrangement shown in figure the bodies have masses m0, m1, m2, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m1. Look into possible cases.

View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1

View SolutionConsider the situation as shown in the figure . The masses of pulley and the threads , as well as the friction in the pulley , are negligible. Assuming both bodies to be motionless at the initial moment. Find the mass ratio m1/m2 at which the body m2
(a) starts coming down
(b) starts going up
( c) is at rest

View SolutionThe following parameters of the arrangement of figure are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down,
(b) starts going up,
(c) is at rest.
View Solution

