Prism 1 with bar 2 of mass m placed on it gets a horizontal acceleration w directed to the left (figure). At what maximum value of this acceleration will the bar still stationary relative to the prism, if the coefficient of friction between them k<cotα ?

On the basis of the initial argument of the solution of above, the tendency of bar 2 with respect to 1 will be to move up along the plane.
Let us fix (x−y) coordinate system in the frame of ground as shown in figure.
From second law of motion in projection form along y and x-axis:
mgcosα−N=mwsinα
or, N=m(gcosα−wsinα) (1)
mgsinα+fr=mwcosα
or, fr=m(wcosα−gsinα) (2)
but fr≤kN, so from (1) and (2)
(wcosα−gsinα)≤k(gcosα+wsinα)
or, w(cosα−ksinα)≤g(kcosα+sinα)
or, w≤g(cosα+sinα)cosα−ksinα,
So, the sought maximum acceleration of the wedge:
wmax=(kcosα+sinα)gcosα−ksinα=(kcotα+1)gcotα−k where cotα>k

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A plank of mass m1 with a bar of mass m2 placed on it lies on a smooth horizontal plane. A horizontal force growing with time t as F′=at (a is constant) is applied to the bar. Find how the accelerations of the plank w1 and of the bar w2 depend on t, if the coefficient of friction between the plank and the bar is equal to k. Draw the approximate plots of these dependences.
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View Solution
Knowledge Check
Determine the maximum acceleration of the train in , which a box lying on its floor will remain stationary, given that the coefficient of static friction between the -box and the train floor is 0.15 (given g=10m/s2)
A1m/s2B1.5m/s2C2m/s2D0
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionA block of mass M = 4 kg is kept on a smooth horizontal plane. A bar of mass m = 1 kg is kept on it. They are connected to a spring as shown & the spring is compressed. Then what is the maximum compression in the spring for which the bar will not slip on the block when released if coefficient of friction between them is 0.2 & spring constant = 1000 N/m : (Take g=10m/s2)

View SolutionTwo block , with masses m1 and m2 are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle α below the horizontal . The coefficient of friction between m1 and m2 are μs
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together

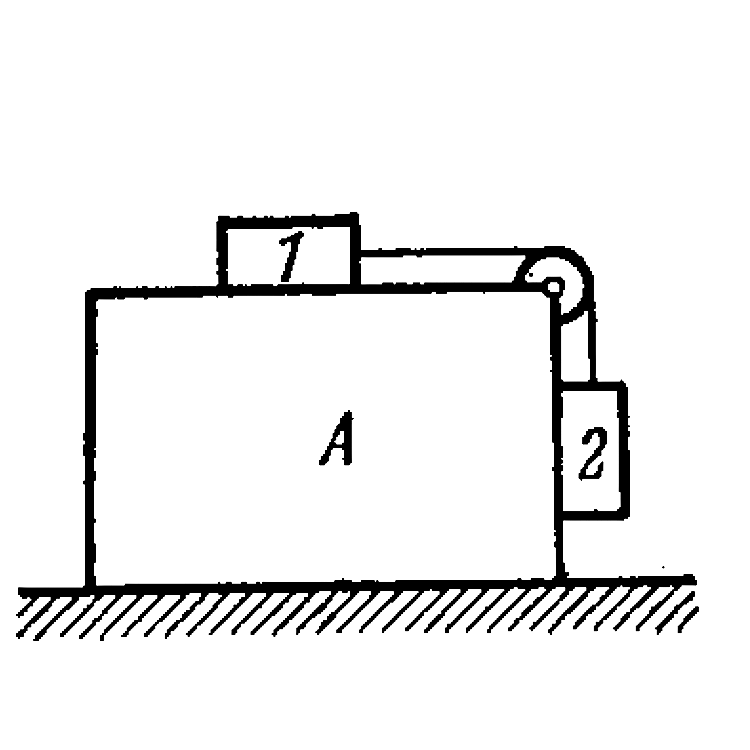
View SolutionWhat is the minimum acceleration with which bar A (figure) should be shifted horizontally to keep bodies 1 and 2 stationary relative to the bar? The masses of the bodies are equal, and the coefficient of friction between the bar and the bodies is equal to k. The masses of the pulley and the threads are negligible, the friction in the pulley is absent.
View SolutionA block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View SolutionTwo touching bars 1 and 2 are placed on an inclined plane forming an angle α with the horizontal (figure). The masses of the bars are equal to m1 and m2, and the coefficients of friction between the inclined plane and these bars are equal to k1 and k2 respectively, with k1>k2. Find:
(a) the force of interaction of the bars in the process of motion,
(b) the minimum value of the angle α at which at bars start sliding down.

View SolutionMass m2 placed on a plank of mass m1lying on a smooth horizontal plane. A horizontal force F=α0t ( α0 is a constant ) is applied to a bar. If acceleratiion of the plank and bar are a1 and a2 respectively and the coefficient of friction between m1 and m2 is μ. Then find acceleration a with time t.
View Solution

