A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
The force with which the cylinder wall acts on the particle will provide centripetal force necessary for the motion of the particle, and since there is no acceleration acting in the horizontal direction, horizontal component of the velocity will remain constant throughout the motion.
So vx=v0cosα
Using, Fn=mwn, for the particle of mass m,
N=mv2xR=mv20cos2αR
which is the required normal force.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View SolutionA particle moves from rest at A on the surface of a smooth circular cylinder of radius r as shown. At B it leaves the cylinder. Find the value of 4cosα3sinβ
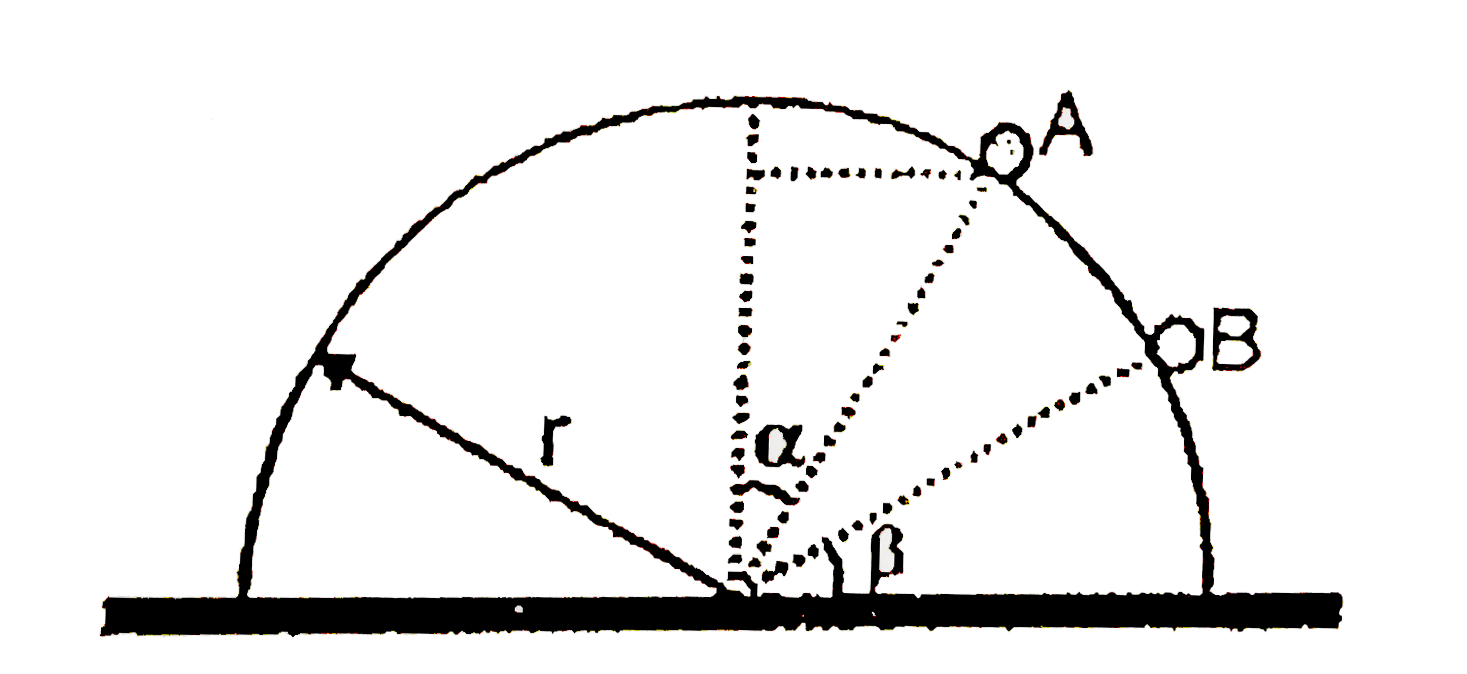
View Solution
Knowledge Check
A particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
AmV20Rsin2αBmV202Rcos2αC2mV20Rcos2αDmV20Rcos2αA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
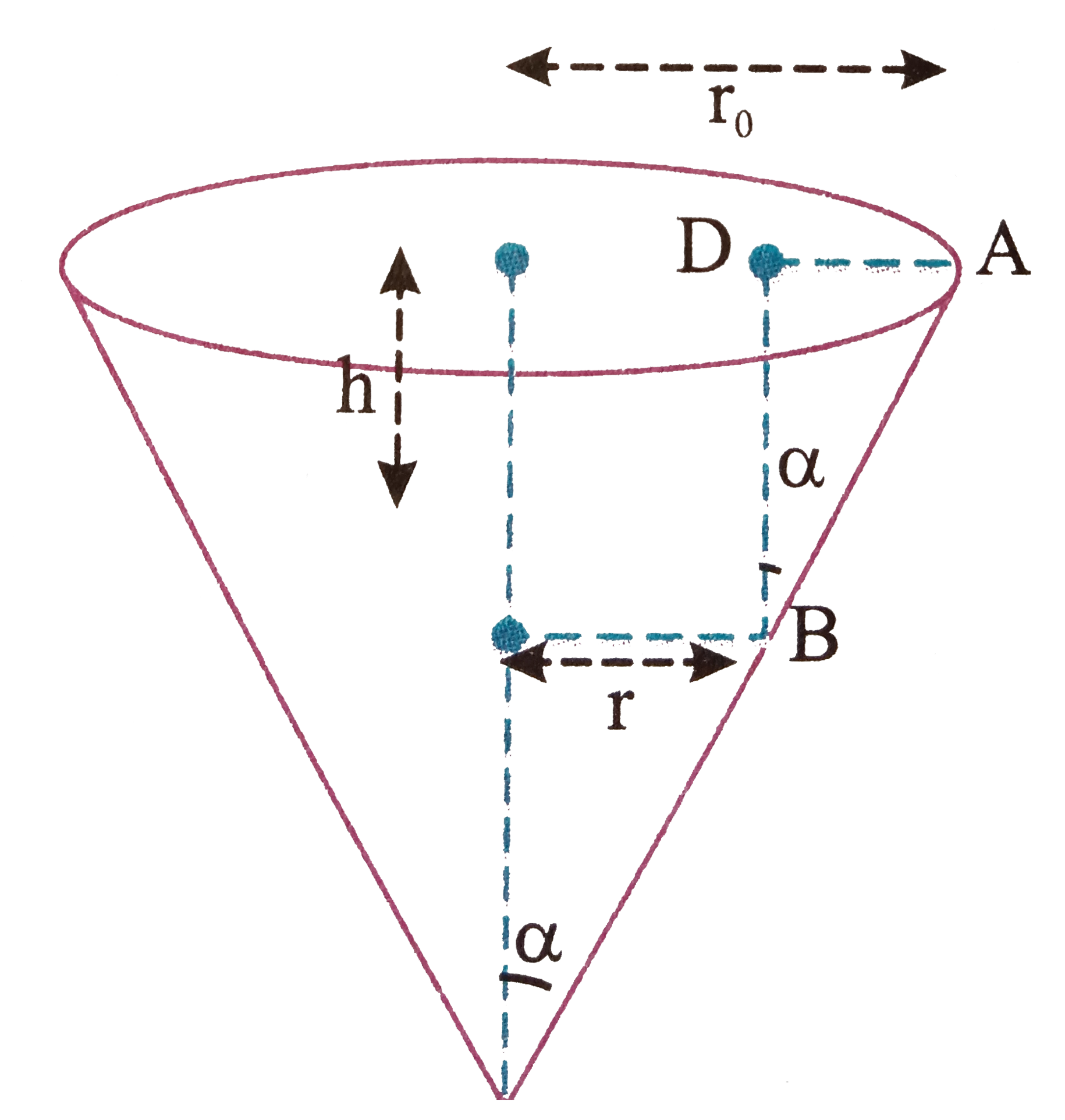 A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanαA ball of mass 1 kg moves inside a smooth fixed spherical shell of radius 1 m with an initial velocity v=5m/s from the bottom. What is the total force acting on the particle at point B
 A10 NB25 NC5√5 ND5 N
A10 NB25 NC5√5 ND5 N
A heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v0 At what point will the particle leave the surface of the hemisphere ? Also determine the value of v0 for which the particle will leave the sphere at the initial instant.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA particle of mass m moves along a circle of radius R. Find the modulus of the average vector of the force acting on the particle over the distance equal to a quarter of the circle, if the particle moves
(a) uniformly with velocity v,
(b) with constant tangential acceleration wτ, the initial velocity being equal to zero.
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v.
View Solution

