A fixed pulley carries a weightless thread with masses m1 and m2 at its ends. There is friction between the thread and the pulley. It is such that the thread starts slipping when the ratio m2/m1=η0 find :
(a) The friction coefficient
(b) The acceleration of the mass when m2/m1=η>η0
Let, us consider a small element of the thread and draw free body diagram for this element.
(a) Applying Newton's second law of motion in projection form, Fn=mwn for this element,
(T+dT)sin(dθ/2)+Tsin(dθ/2)−dN=dmω2R=0
or, 2Tsin(dθ/2)=dN, [neglecting the term ( dTsinθ/2)]
or, Tdθ=dN, as sin(dθ)2=dθ2 (1)
Also, dfr=kdN=(T+dT)−T=dT (2)
From Eqs. (1) and (2),
kTdθ=dT or dTT=kdθ
In this case Q=π so,
or, or, 1nT2T1=kπ (3)
So, k=1π1nT2T1=1πη0
as T2T1=m2gm1g=m2m1=η0
(b) When m2m1=η, which is greater than η0, the blocks will move with same value of acceleration. (say w) and clearly m2 moves downward. From Newton's second law in projection form (downward for m2 and upward for m1) we get:
m2g−T2=m2w (4)
and T1−m1g=m1w (5)
Also T2T1=η0 (6)
Simultaneous solution of Eqs. (4), (5) and (6) yields:
w=(m2−η0m1)g(m2+η0m1)=(η−η0)(η+η0)g (as m2m1=η)

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A fixed pulley carries a weightless thread with masses m2andm1 at its ends (m2>m1). There is friction between the thread and the pulley. If it is such that the thread starts slipping when the ratio of m2 to m1 is n0. Find :
(a) the friction coefficient
(b) the acceleration of the masses when m2m1=n>n0
[Hint : Consider an element of the thread of width dθ at angular distance θfrom the horzontal diameter of the pulley. The forces at the ends are T and T = dT. If dN is the normal reaction of the pulley on the element than df (frictional force on the element) =μdN Resolving the tensions at the ends along and perpendicular to the radius vector of the element, we have for equilibrium of the element dT=dfanddN=Tdθ Integrate from T1 to T2.T1=m1gandT2=m2g. These are obtained by considering equilibrium of m1andm2]
View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1

View SolutionFind the acceleration of masses m1 and m2 moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
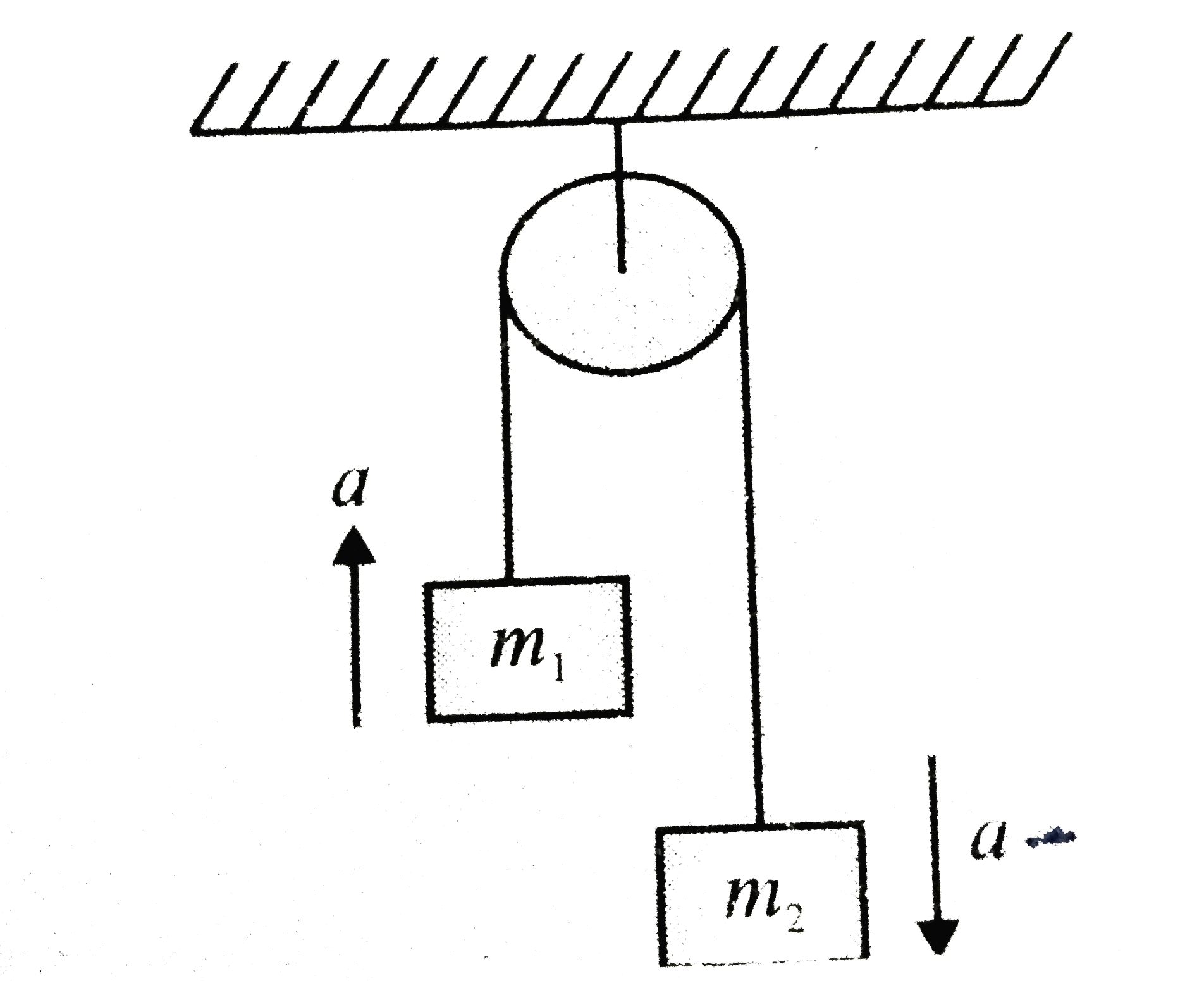
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
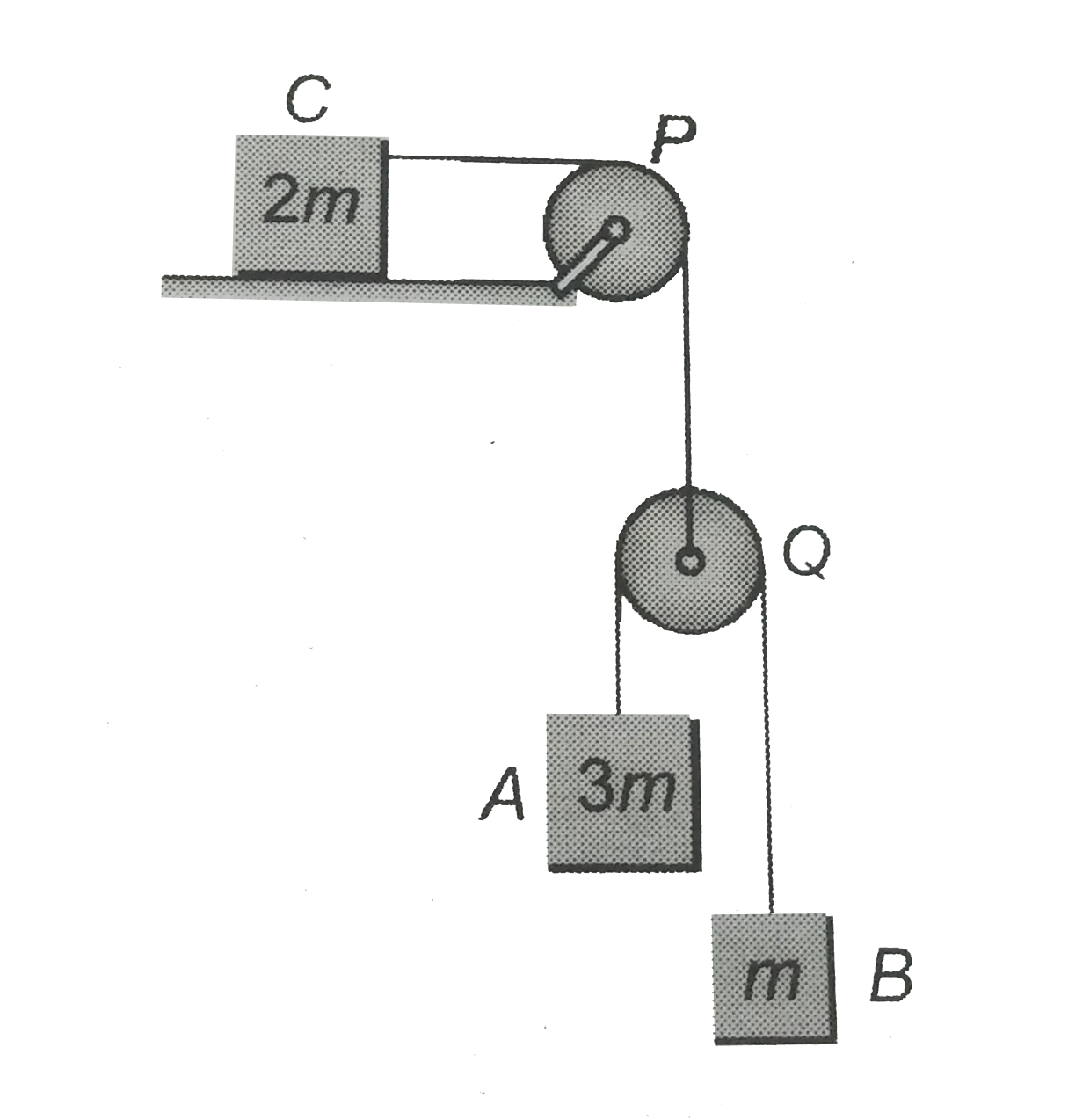
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
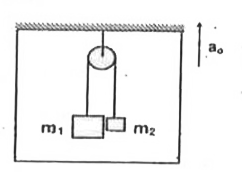
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
View SolutionFind the acceleration of m1 and m2 in an Atwood's Machine if there is friction present between surface of pulley and the thread and thread does not slip over the surface ofpulley. Moment of inertia of pulley is I.
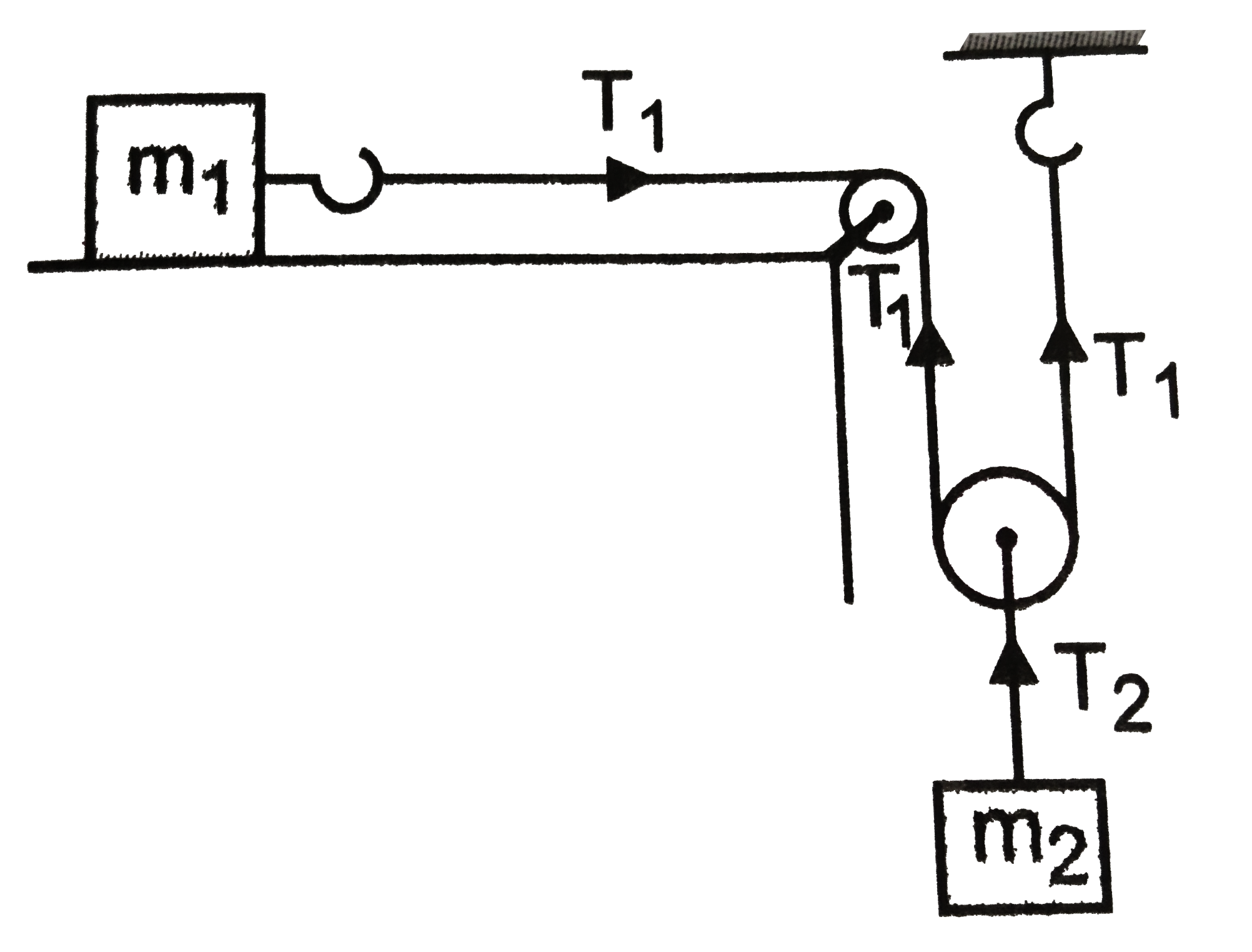
View SolutionWhen we ignore friction and mass of pulley what would be the accelerations of the two blocks m1 and m2
 .
.
View Solution

