A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
The ball has only normal acceleration at the lowest position and only tangential acceleration at any of the extreme position. Let v be the speed of the ball at its lowest position and l be the length of the thread, then according to the problem
v2l=gsinα (1)
wehre α is the maximum deflection angle
From Newton's law in projection form: Ft=mwt
−mgsinθ=mvdvldθ
or, −glsinθdθ=vdv
On integrating both the sides within their limits.
−glα∫0sinθdθ=0∫vvdv
or, v2=2gl(1−cosα) (2)
Note: Eq. (2) can easily be obtained by the conservation of mechanical energy of the ball in the uniform field of gravity.
From Eqs. (1) and (2) with θ=α
2gl(1−cosα)=lgcosα
or cosα=23 so, α=53∘

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that the magnitudes of its acceleration in the extreme and the lowest positions are equal. Find the maximum deflection of the thread with respect to the vertical.
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the magnitude of the force acting on the particle as a function of s.
View SolutionA small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View Solution
Knowledge Check
A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)A ball attached to one end of a stringj swings in a vertical plane such that its acceleration at point A (exterme posiuion) is eqal to its acceleration at point B (mean posirion), The angle θ is
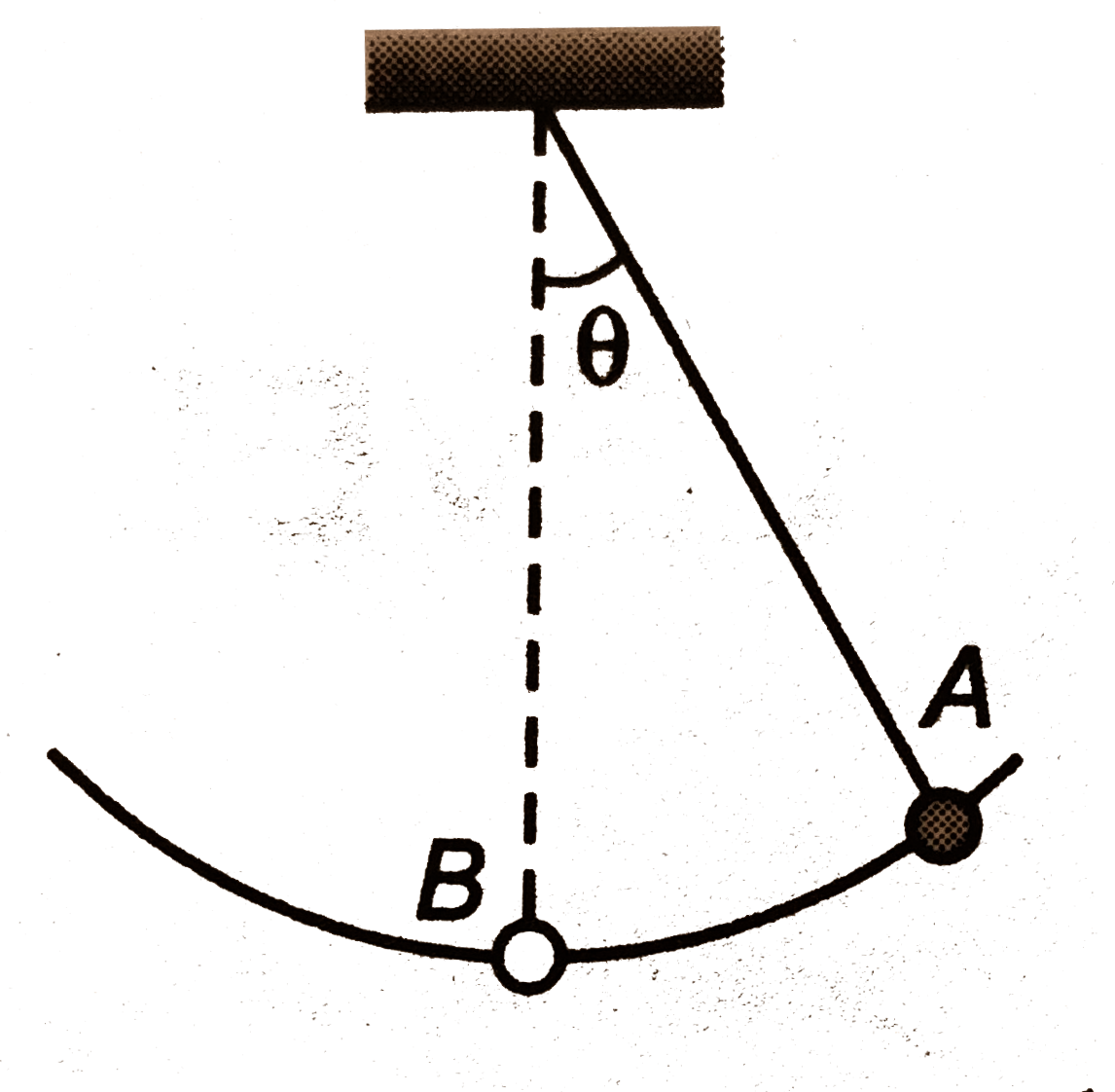 Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of theseParticle moves from extreme position to mean position, its
Akinetic energy increases, potential energy decreasesBkinetic energy decreases, potential increasesCboth remains constantDpotential energy becomes zero and kinetic energy remains contant
A rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionStudy the diagram given below and answer the following question.

Name the extreme position of the swing.
View SolutionThe velocity at mean position and acceleration at the extreme position have the phase difference of
View SolutionA short boy sits on a seat suspended by a light string from a fixed point O and starts swinging in a vertical plane from the extreme position P with a small amplitude the graph which shows the variation of the tension in the string with time 't' is:

View SolutionThe acceleration of a particle performing S.H.M. at extreme position is
View Solution

