The following parameters of the arrangement of figure are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down,
(b) starts going up,
(c) is at rest.
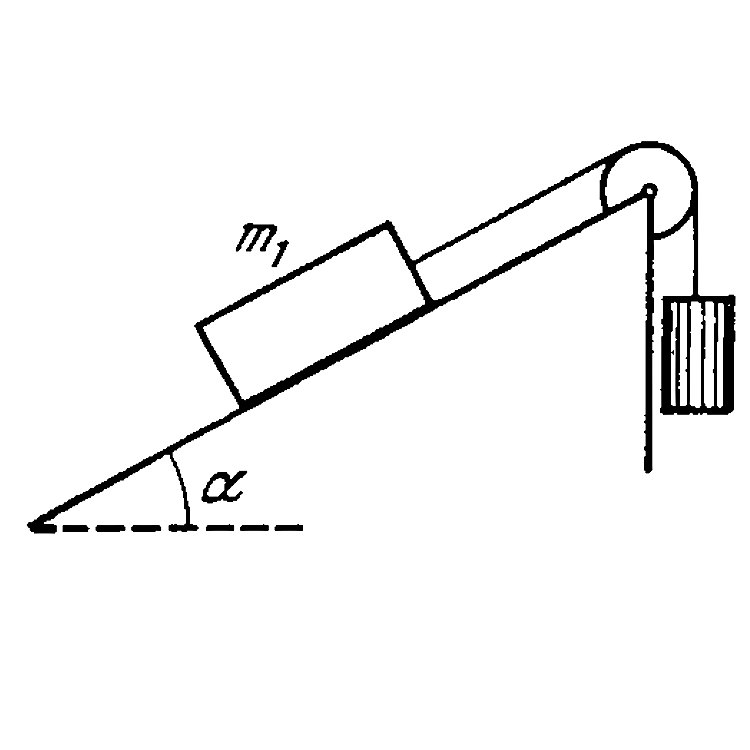
At the initial moment, obviously the tension in the thread connecting m1 and m2 equals the weight of m2.
(a) For the block m2 to come down or the block m1 to go up, the condition is
m2g−T≥0 and T−m1gsinα−≥0
where T is tension and fr is friction which in the limiting case equals km1gcosα. Then
or m2g−m1sinα>km1gcosα
or m2m1>(kcosα+sinα)
(b) Similarly in the case
m1gsinα−m2g>frlim
or, m1sinα−m2g>km1gcosα
or, m2m1<(sinα−kcosα)
(c) For this case, neither kind of motion is possible, and fr need not be limiting.
Hence, (kcosα+sinα)>m2m1>(sinα−kcoaα)

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Consider the situation as shown in the figure . The masses of pulley and the threads , as well as the friction in the pulley , are negligible. Assuming both bodies to be motionless at the initial moment. Find the mass ratio m1/m2 at which the body m2
(a) starts coming down
(b) starts going up
( c) is at rest

View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

View Solution
Knowledge Check
Find the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time great as the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are accumed to be negligible.
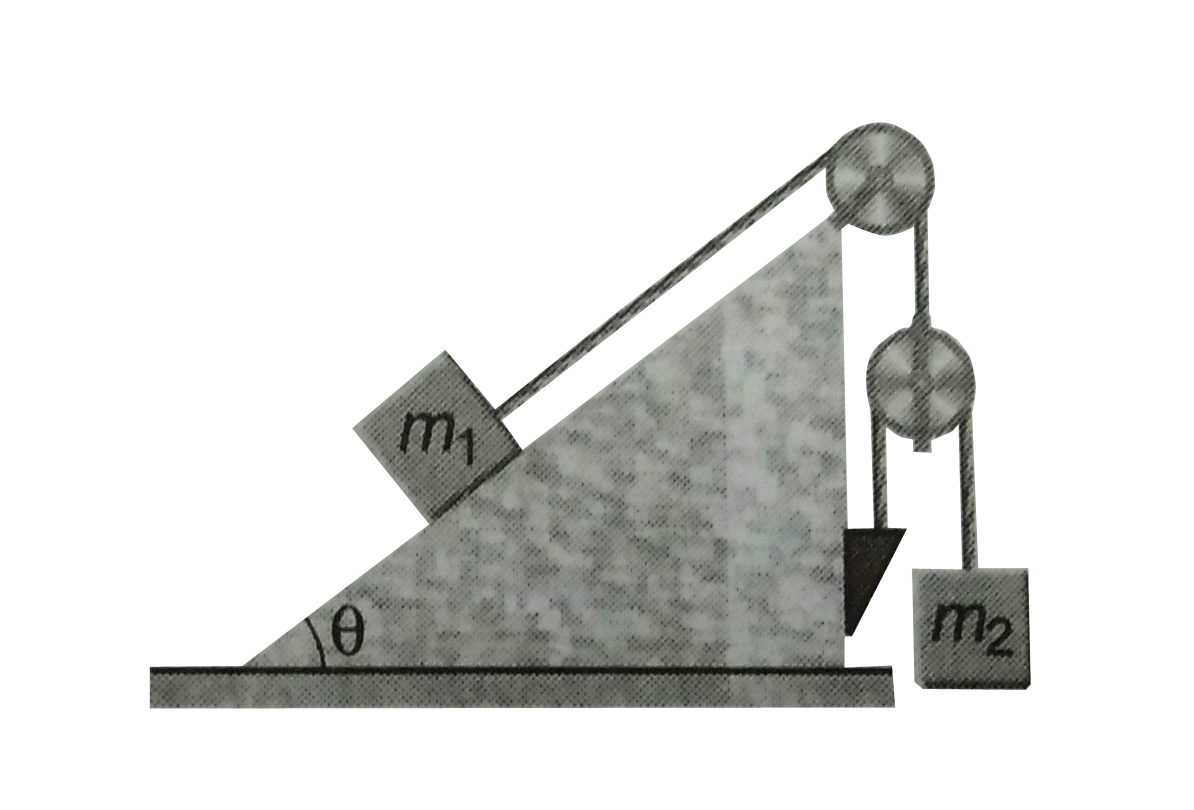 Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1
Ag(2η−sinθ)4η+1B2g(η−sinθ)4η+1C2g(2η−sinθ)η+1D2g(2η−sinθ)4η+1A body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
A1.25ms−2B2.35ms−2C3.4ms−2D4.9ms−2A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
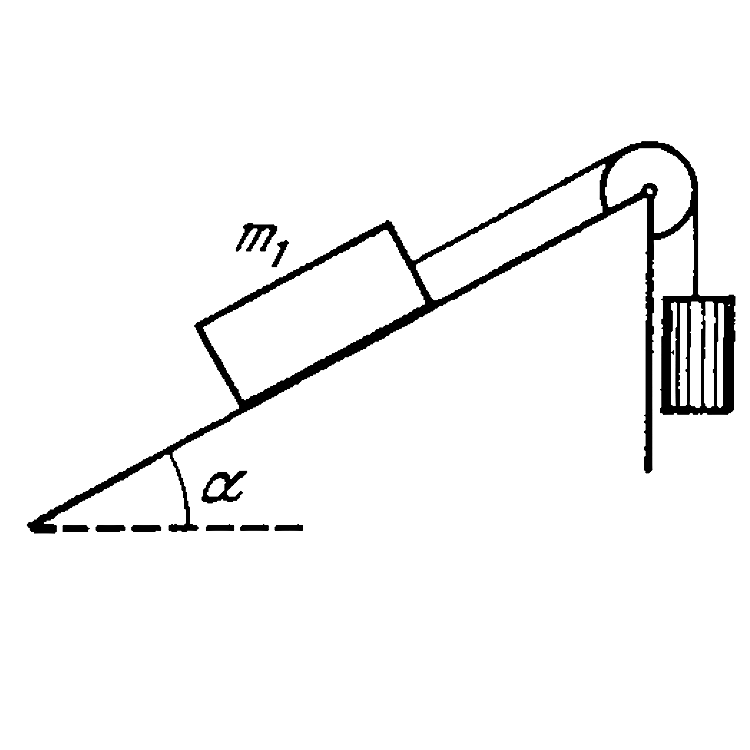
The inclined plane of figure forms an angle α=30∘ with the horizontal. The mass ratio m2/m1=η=2/3. The coefficients of friction between the body m1 and the inclined plane is equal to k=0.10. The masses of the pulley and the threads are negligible. Find the magnitude and the direction of acceleration of the body m2 when the formely stationary system of masses starts moving.
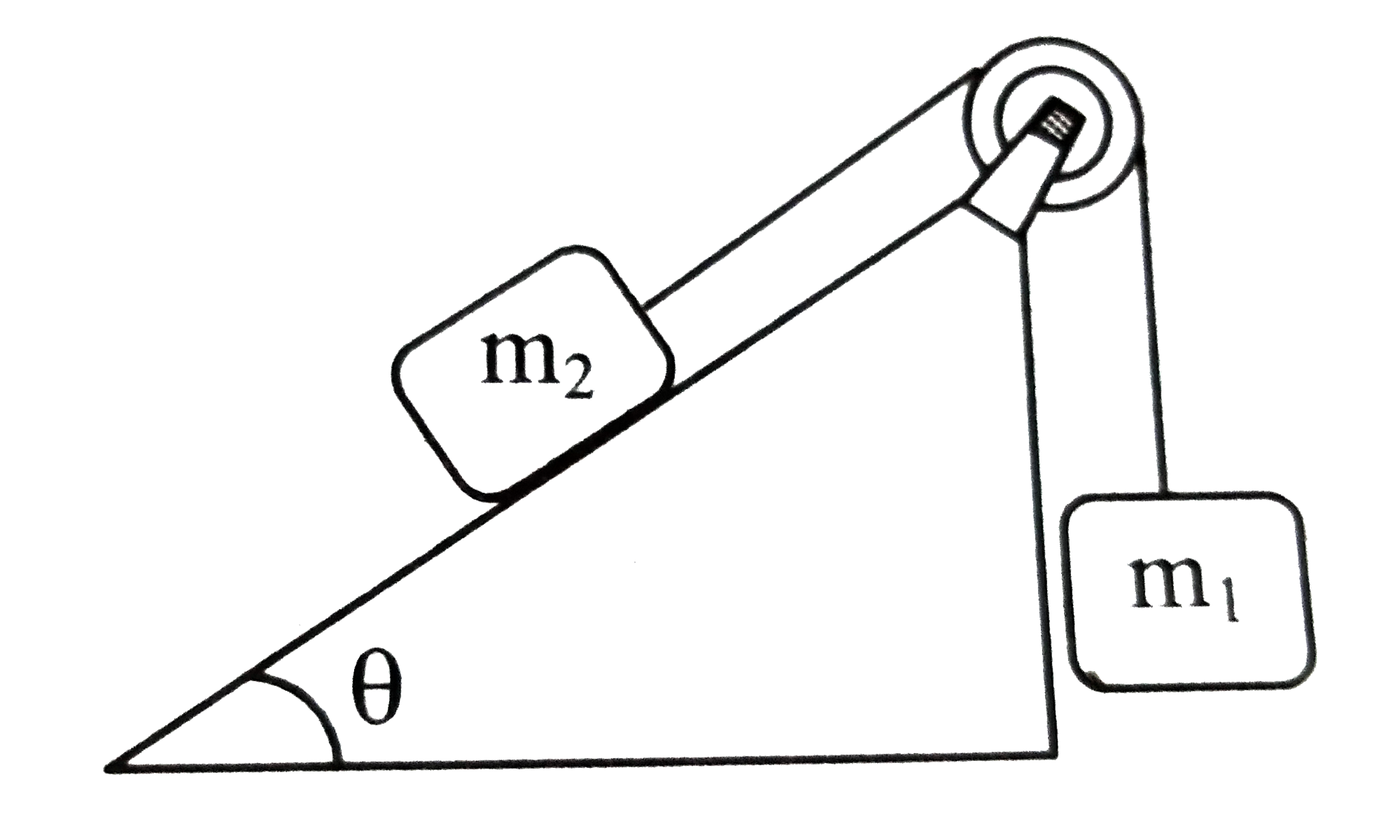
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA body of mass 5×10−3kg is launched upon a rough inclined plane making an angle of 30° with the horizontal. Find the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA body of mass m slides down an inclined plane making an angle of 45∘ with the horizontal. If the coefficient of friction between the body and the plane be 0.3, the acceleration of the body is approximately equal to :
View Solution

