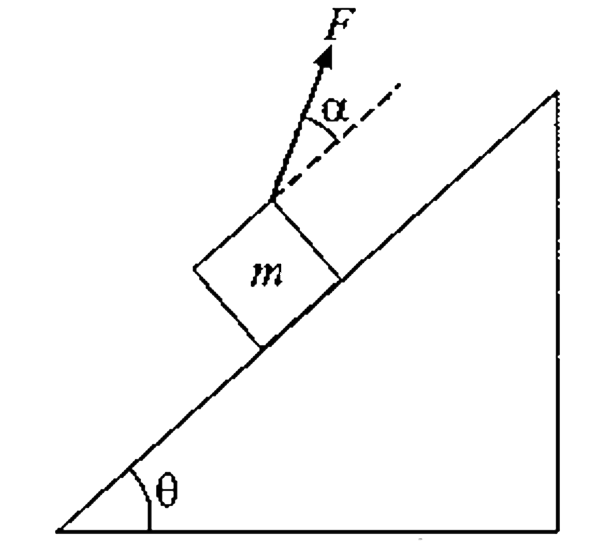
A bar of mass m is pulled by means of a thread up an inclined plane forming an angle $α$ with the horizontal (figure). The coefficient of friction is equal to k. Find the angle $β$ which is thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?

Video Solution

Text Solution

Verified by Experts

Let us fix the $x - y$ co-ordinate system to the wedge, taking the x-axis up, along the incline and the y-axis perpendicular to it (figure).
Now, we draw the free body diagram for the bar.
Let us apply Newton's second law in projection from along x and y axis for the bar:
$T \cos β - m g \sin α - f r = 0$ (1)
$T \sin β + N - m g \cos α = 0$
or, $N = m g \cos α - T \sin β$ (2)
But $f r = k N$ and using (2) in (1), we get
$T = m g \sin α + k m g \cos α / (\cos β + k \sin β)$ (3)
For $T_{min}$ the value of $(\cos β + k \sin β)$ should be maximum
So, $\frac{d (\cos β + k \sin β)}{d β} = 0$ or $\tan β = k$
Putting this value of $β$ in Eq. (3) we get,
$T_{min} = \frac{m g (\sin α + k \cos α)}{1 / \sqrt{1 + k^{2}} + k^{2} / \sqrt{1 + k^{2}}} = \frac{m g (\sin α + k \cos α)}{\sqrt{1 + k^{2}}}$

Updated on:21/07/2023

A body is sliding down an inclined plane forming an angle $30^{\circ}$ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
A $1.25 m s^{- 2}$
B $2.35 m s^{- 2}$
C $3.4 m s^{- 2}$
D $4.9 m s^{- 2}$
A body is sliding down an inclined plane forming an angle $30^{\circ}$ with the horizantal. If the coefficient of friction is $0.3$ then acceleration of the body is
A $1.25 . m s^{- 2}$
B $2.35 m s^{- 2}$
C $3.4 m s^{- 2}$
D $4.9 m s^{- 2}$
A body of mass m slides down an inclined plane making an angle of $45^{\circ}$ with the horizontal. If the coefficient of friction between the body and the plane be 0.3, the acceleration of the body is approximately equal to :
A0.22 g
B0.30 g
C0.49 g
D0.70 g