A small body A starts sliding down from the top of a wedge (figure) whose base is equal to l=2.10m. The coefficient of friction between the body and the wedge surface is k=0.140. At what value of the angle α will the time of sliding be the least? What will it be equal to?
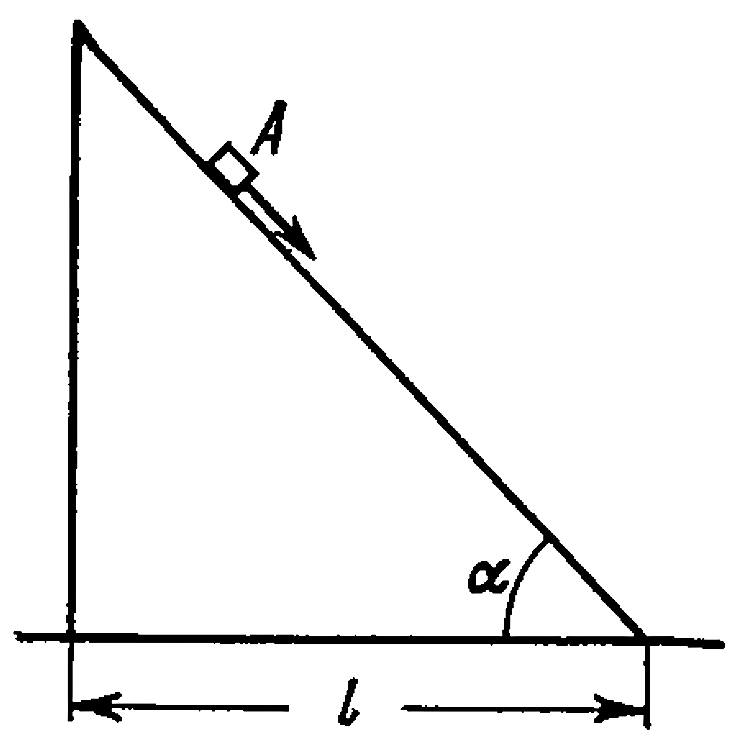
Let us designate the x-axis (figure) and apply Fx=mwx for body A:
mgsinα−kmgcosα=mw
or, w=gsinα−kgcosα
Now, from kinematical equation:
lsecα=0+(1/2)wt2
or, t=√2lsecα/(sinα−kcosα)g
=√2l/(sin2α/2−kcos2α)g
(using Eq. (1)).
for tmin' d(sin2α2−kcos2α)dα=0
i.e. 2cos2α2+2kcosαsinα=0
or, tan2α=−1k⇒α=49∘
and putting the values of α, k and l in Eq. (2) we get tmin=1s.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A small body A starts sliding down from the top of a wedge (see fig) whose base is equal to l. The coefficient of friction between the body and wedge surface is μ=1.0. At what value of angle q will the time of sliding be least?
View SolutionA block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
View Solution
Knowledge Check
A body of mass m slides down an inclined plane making an angle of 45∘ with the horizontal. If the coefficient of friction between the body and the plane be 0.3, the acceleration of the body is approximately equal to :
A0.22 gB0.30 gC0.49 gD0.70 gA block is at rest on an inclined plane making an angle α with the horizontal . As the angle α of the incline is increased the block starts slipping when the angle of inclination becomes θ. The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle θ to the horizontal. Then the coefficient of friction is equal to
AsinθBcosθCtanθDIndependent of θCoefficient of friction between block of mass m and fixed wedge is μ=0.5. For what value of mM frictional force between block of mass m and wedge becomes zero ?
 A12B2C1DNone of these
A12B2C1DNone of these
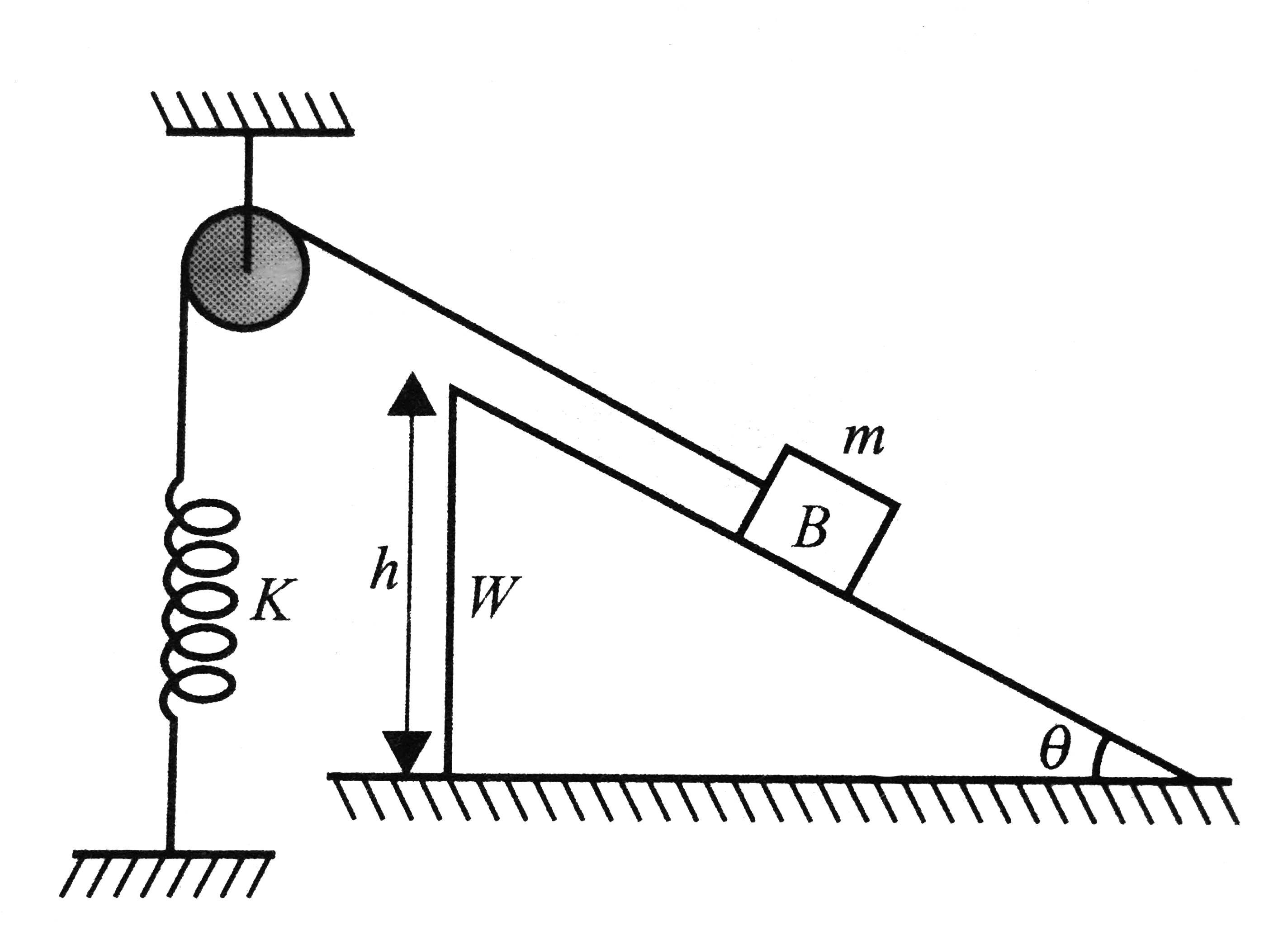
In figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?

View SolutionA body is sliding down a rough inclined plane The coefficient of friction between the body and the plane is 0.5.The ratio of the net force required for the body to slide down and the normal reaction on the body is 1:2 Then the angle of the inclined plane is
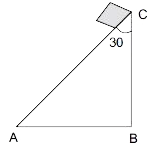
View SolutionA body of mass M starts sliding down an Inclined plane where critical angle is <ACB=30∘ as shown in figure, the coefficient of friction will be
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
View Solution

