A bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
Newton's second law of motion in projection form, along horizontal or x-axis i.e.
Fx=mwx gives.
Fcos(as)=mvdvds (as α=as)
or, Fcos(as)ds=mvdv
Integrating, over the limits for v(s)
Fm∞∫0cos(as)ds=v22
or v=√2Fsinαma
=√2gsinα/3a (using F=mg3)
which is the sought relationship.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
View SolutionA small bar starts sliding down an inclined plane forming an angle α with the horizontal. The friction coefficient depends on the distance x covered as k=ax, where a is a constant. Find the distance covered by the bar till it stops, and its maximum velocity over this distance.
View Solution
Knowledge Check
A block is resting over a smooth horizontal plane. A constant horizontal force starts acting on it at t=0. Which of the following graph is correct:
A B
B C
C D
D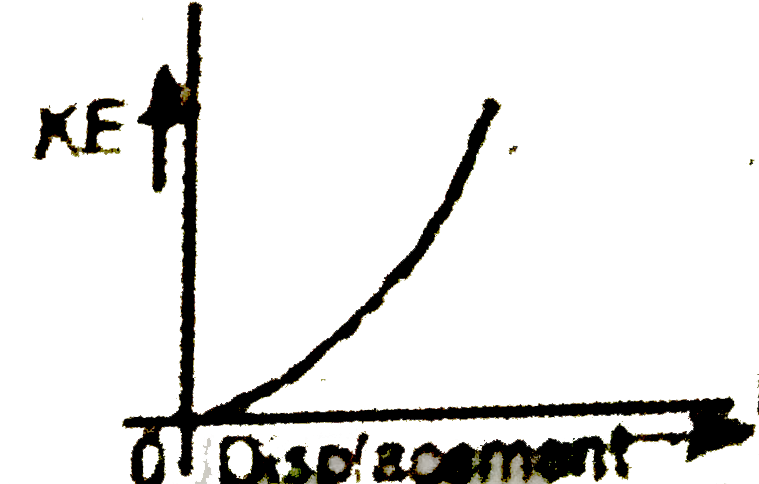
A body of mass m starts moving from rest along x-axis so that it velocity varies as v=a√s where a is a constant and s is the distance covered by the body .The total work done by all the forces acting on the body in the first second after the start of the motion is :
A18ma4t2B4ma4t2C8ma4t2D14ma4t2A force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
AFmωsin(ωt2)B2Fmωsin(ωt2)CF2mωsin(ωt2)D2F3mωsin(ωt2)
A point moves along an arc of a circle of radius R. Its velocity depends on the distance covered s as v=√s, where a is a constant. Find the angle α between the vector of the total acceleration and the vector of velocity as a function of s.
View SolutionA body of mass m rests on a horizontal plane with the friction coefficient k. At the moment t=0 a horizontal force is applied to it, which varies with time as F=at, where a is a constant vector.
Find the distance traversed by the body during the first t seconds after the force action began.
View SolutionA locomotive of mass m starts moving so that its velocity varies according to the law V=α√s, where α is a constant and s is the distance covered. Find the total work done by all the forces acting on the locomotive during the first t seconds after the beginning of motion.
View SolutionA locomotive of mass 'm' starts moving so that its velocity varies as v=αs23 where α is a positive constant and 's' is the distance travelled .The total work done by all the forces acting on the locomotive during first 't' second after the start of motion is
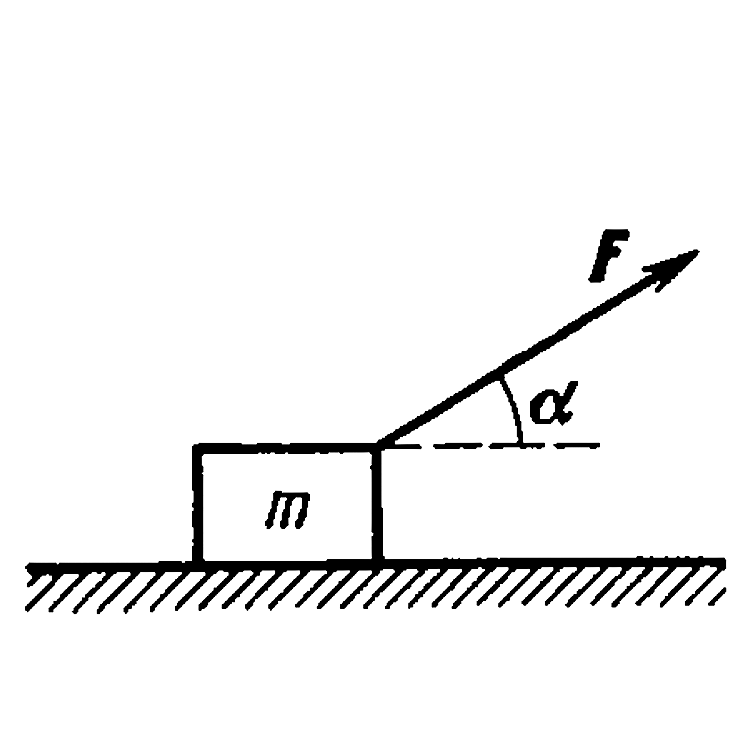
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View Solution

