A point source of monochromatic light 'S' is kept at the centre of the bottom of a cylinder of radius . The cylinder contains water (refractive index 4//3) to a height of . Draw the ray diagram and calculate the area of water surface through which the light emerges in air.
The correct Answer is:
To solve the problem step by step, we will follow these procedures:
Step 1: Understand the Setup
We have a point source of monochromatic light 'S' located at the center of the bottom of a cylinder filled with water. The cylinder has a radius of 15.0 cm and a height of 7.0 cm. The refractive index of water is given as 43.
Step 2: Draw the Ray Diagram
1. Draw a vertical cylinder with a radius of 15 cm and a height of 7 cm.
2. Mark the center of the bottom of the cylinder as point 'S'.
3. Draw rays emanating from point 'S' towards the water surface at various angles.
Step 3: Determine the Critical Angle
The light is transitioning from a denser medium (water) to a rarer medium (air). The critical angle C can be calculated using Snell’s law:
sinC=nairnwater
Given that nair=1 and nwater=43:
sinC=143=34
Step 4: Calculate the Critical Angle
To find the critical angle C:
C=arcsin(34)
Step 5: Use Geometry to Find the Radius of the Emerging Circle
Using the geometry of the situation, we can relate the radius R of the circle through which light emerges to the height of the water:
tanC=Rh
Where h=7cm. From the triangle formed:
tanC=sinCcosC
We already have sinC=34. To find cosC, we use:
cos2C+sin2C=1⟹cos2C=1−(34)2=1−916=716⟹cosC=√74
Thus,
tanC=34√74=3√7
Now substituting back:
R7=3√7⟹R=7⋅3√7=21√7=3√7cm
Step 6: Calculate the Area of the Emerging Circle
The area A of the circle through which light emerges is given by:
A=πR2
Substituting R=3√7:
A=π(3√7)2=π⋅9⋅7=63πcm2
Final Answer
The area of the water surface through which the light emerges in air is 63πcm2.
---
We have a point source of monochromatic light 'S' located at the center of the bottom of a cylinder filled with water. The cylinder has a radius of 15.0 cm and a height of 7.0 cm. The refractive index of water is given as 43.
1. Draw a vertical cylinder with a radius of 15 cm and a height of 7 cm.
2. Mark the center of the bottom of the cylinder as point 'S'.
3. Draw rays emanating from point 'S' towards the water surface at various angles.
The light is transitioning from a denser medium (water) to a rarer medium (air). The critical angle C can be calculated using Snell’s law:
sinC=nairnwater
Given that nair=1 and nwater=43:
sinC=143=34
To find the critical angle C:
C=arcsin(34)
Using the geometry of the situation, we can relate the radius R of the circle through which light emerges to the height of the water:
tanC=Rh
Where h=7cm. From the triangle formed:
tanC=sinCcosC
We already have sinC=34. To find cosC, we use:
cos2C+sin2C=1⟹cos2C=1−(34)2=1−916=716⟹cosC=√74
Thus,
tanC=34√74=3√7
Now substituting back:
R7=3√7⟹R=7⋅3√7=21√7=3√7cm
The area A of the circle through which light emerges is given by:
A=πR2
Substituting R=3√7:
A=π(3√7)2=π⋅9⋅7=63πcm2
The area of the water surface through which the light emerges in air is 63πcm2.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(c)
Explore 27 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Long Answer (a)
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A point source of monochromatic light 'S' is kept at the centre of the bottom of a cylinder of radius 15.0cm. The cylinder contains water (refractive index 4//3) to a height of 7.0cm. Draw the ray diagram and calculate the area of water surface through which the light emerges in air.
View SolutionA point source of light is 80.0cm below the surface of a body of water. Find the diameter of the circle at the surface through which light emerges from the water.
View Solution
Knowledge Check
The focal length of lens of refractive index 1.5in air is30cmWhen it is immersed in water of refractive index43,then its focal length will be
A120cmB60cmC30cmD240cmThe optical path of a monochromatic light is same if it goes through 4.0cm of glass of 4.5cm of water. If the refractive index of glas is 1.53, the refractive index of the water is
A1.30B1.36C1.42D1.46The optical path of a monochromatic light is same if it goes through 4.0 cm of glass or 4.5 cm of water. If the refractive index of glass is 1.53, the refractive index of the water is
A1.30B1.36C1.42D1.46
A point light source is attached to the base of an empty trough. A transparent liquid of refractive index 1.35 is filled in the trough to a height of 50 cm. Calculate the total area on the surface of the liquid through which light will emerge.
View SolutionA liquid of refractive index 1.5 is poured into a cyclindrical jar of radius 20 cm upto a height of 20 cm. A small bulb at the centre of bottom glowing. Find area of the liquid surface through which the light of the bulb passes into air.
View SolutionThe optical path of monochromatic light is same if it travels 2cm thickness of glass or 2.25cm, thickness of water. If refractive index of glass is 1.5, what is the refractive index of water ?
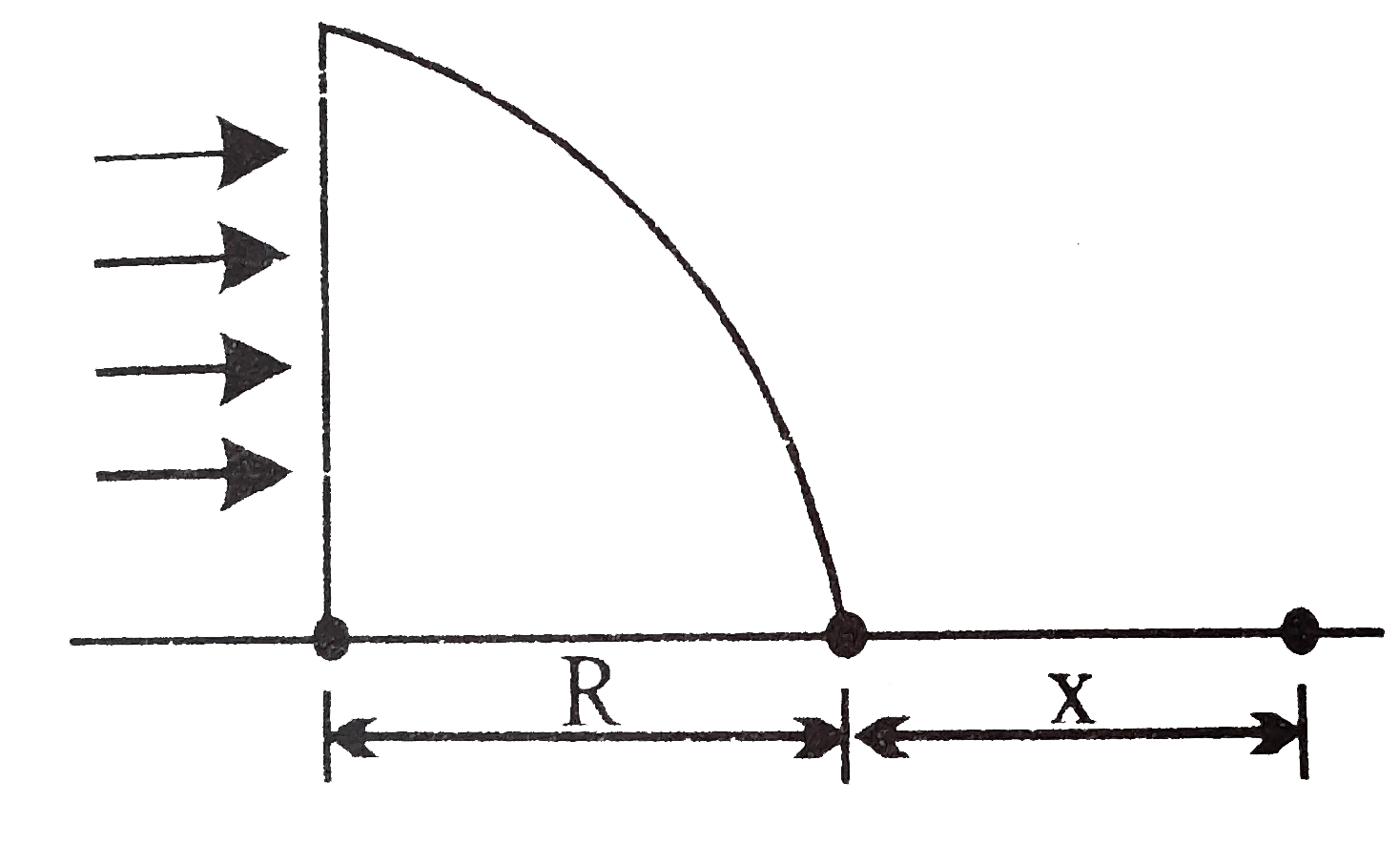
View SolutionA uniform,horizontal beam of light is incident upon a quarter cylinder of radiusR=5cm and has a refractive index 2/√3.A patch on the table for a distance 'x'from the cylinder is unilluminated ,find the value of 'x'?
View SolutionA point source of light is kept on the surface of a sphere and it is found that parallel light rays emerge from the other side of the sphere. What is refractive index of material of the sphere ?
View Solution

