A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ?
The correct Answer is:−266cm
Here, μ1=1.33,μ2=1.48,u=?,v=∞
R=30cm
Refraction from rarer to denser medium
−μ1u+μ2v=μ2−μ1R
−1.33u+1.48∞=1.48−1.3330=0.1530=1200
u=−200×1.33=−266cm.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(c)
Explore 27 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Long Answer (a)
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A spherical surface of radius 30cm separates two transparent media A and B with refractive indiecs 1.33 and 1.48 , respectively. The medium A is on the convex side of the surface. Where should a point object the placed in medium A so that the paraxial rays become parallel after refraction at the surface?
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution
Knowledge Check
A concave spherical surface of radius of curvature 10cm separates two mediums X and Y of refractive indices 4/3 and 3/2 respectively. Centre of curvature of the surfaces lies in the medium X. An object is placed in medium X.
AImage is always realBImage is real if the object distance is greater than 90cmCImage is always virtualDImage is virtual only If the object distance is less than 90cm.A concave spherical surface of radius of curvature 10 cm separates two medium x & y of refractive index 4/3 & 3/2 respectively. If the object is placed along principal axis in medium X then
 Aimage is always realBimage is real if the object distance is greater than 90cmCimage is always virtualDimage is virtual if the object distance is less than 90 cm
Aimage is always realBimage is real if the object distance is greater than 90cmCimage is always virtualDimage is virtual if the object distance is less than 90 cmA spherical convex surface separates object and image space of refractive index 1 and 43 respectively. If radius of curvature of the surface is 0.1 m, its power is
A2.5DB-2.5 DC3.3DD-3.3D
A convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
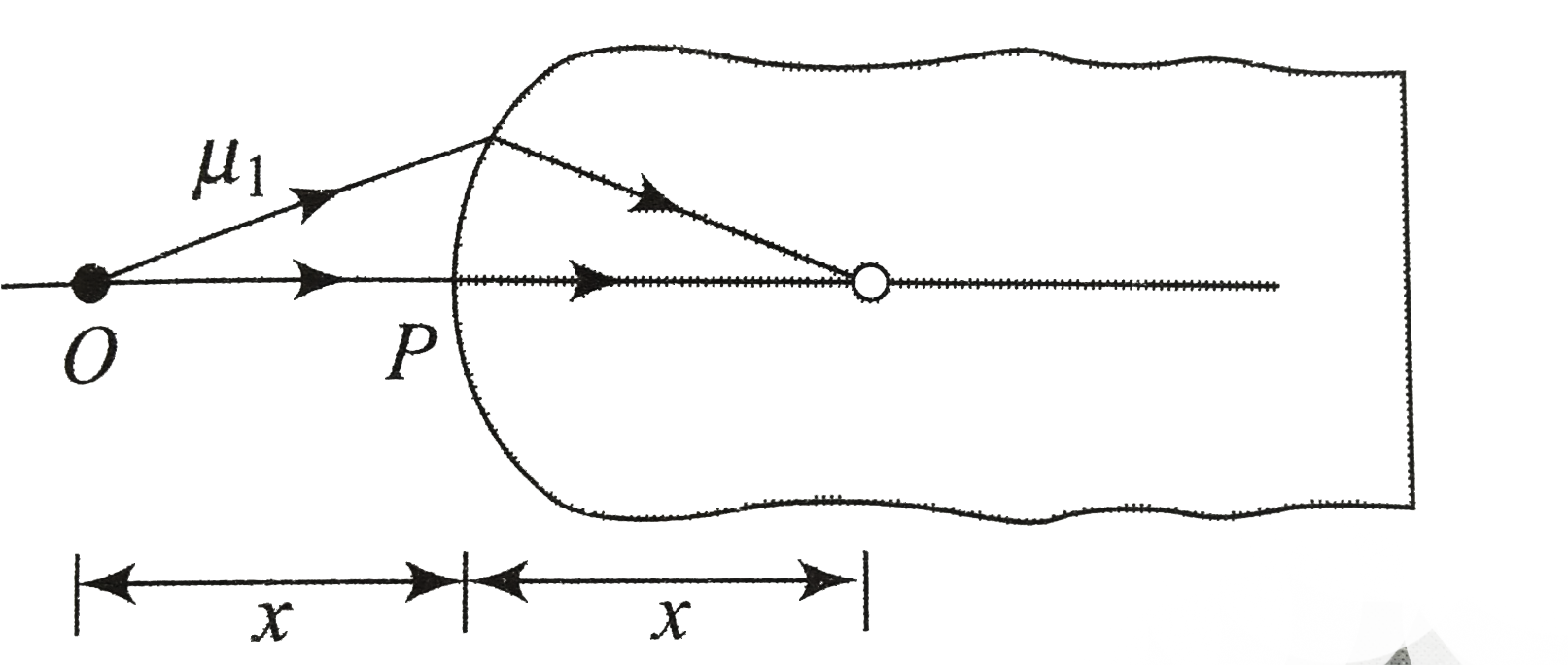
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionA concave spherical surface of radius of curvature R=20cm separates two media A and B having refractive indices μA=43 and μB=32respectively. A point object is placed on the principal axis. Find the distance of the object from the surface so that its image is virtual when
(a) the object is in medium A.
(b) the object is in medium B.
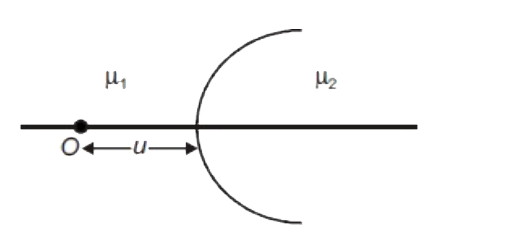
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionThree transparent media of refractive indices μ1,μ2,μ(3) respectively, are stacked as shown. A ray of light follows the path shown. No light enters the third medium.
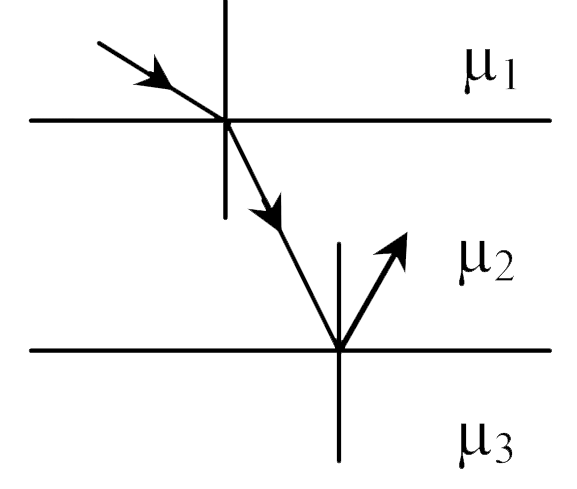
Then-
View Solution

