An air bubble in a glass sphere (μ=1.5) is situated at a distance 3cm from a convex surface of diameter 10cm. At what distance from the surface will the bubble appear ?
The correct Answer is:−2.5cm
To solve the problem, we need to determine the apparent position of the air bubble when viewed from outside the glass sphere. We will use the lens maker's formula for refraction at a spherical surface.
1. Identify Given Values:
- Refractive index of glass, μ=1.5
- Distance of the bubble from the convex surface, u=−3cm (the object distance is taken as negative in the sign convention for refraction)
- Radius of curvature of the convex surface, R=+5cm (positive because it is a convex surface)
2. Use the Refraction Formula:
The formula for refraction at a spherical surface is given by:
μ2v−μ1u=μ2−μ1R
Here, μ1=1 (refractive index of air), μ2=1.5 (refractive index of glass).
3. Substitute the Values:
Substituting the values into the formula:
1.5v−1−3=1.5−15
4. Simplify the Equation:
This simplifies to:
1.5v+13=0.55
1.5v+13=0.1
5. Isolate 1.5v:
Rearranging gives:
1.5v=0.1−13
To combine the fractions, convert 0.1 to a fraction:
0.1=110
Now find a common denominator for 110 and 13:
110−13=3−1030=−730
Thus,
1.5v=−730
6. Solve for v:
Rearranging gives:
v=1.5×30−7=−457≈−6.43cm
7. Interpret the Result:
The negative value of v indicates that the bubble appears to be located at approximately 6.43cm on the same side as the observer, which means it appears to be 6.43cm away from the surface of the glass.
Final Answer:
The bubble will appear to be approximately 6.43cm from the surface of the glass sphere.
- Refractive index of glass, μ=1.5
- Distance of the bubble from the convex surface, u=−3cm (the object distance is taken as negative in the sign convention for refraction)
- Radius of curvature of the convex surface, R=+5cm (positive because it is a convex surface)
The formula for refraction at a spherical surface is given by:
μ2v−μ1u=μ2−μ1R
Here, μ1=1 (refractive index of air), μ2=1.5 (refractive index of glass).
Substituting the values into the formula:
1.5v−1−3=1.5−15
This simplifies to:
1.5v+13=0.55
1.5v+13=0.1
Rearranging gives:
1.5v=0.1−13
To combine the fractions, convert 0.1 to a fraction:
0.1=110
Now find a common denominator for 110 and 13:
110−13=3−1030=−730
Thus,
1.5v=−730
Rearranging gives:
v=1.5×30−7=−457≈−6.43cm
The negative value of v indicates that the bubble appears to be located at approximately 6.43cm on the same side as the observer, which means it appears to be 6.43cm away from the surface of the glass.
The bubble will appear to be approximately 6.43cm from the surface of the glass sphere.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(c)
Explore 27 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Long Answer (a)
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
An air bubble in a glass sphere (μ=1.5) is situated at a distance 3cm from a convex surface of diameter 10cm. At what distance from the surface will be the bubble appear ?
View SolutionAn air bubble in glass (μ=3/2) is situated at a distance of 2 cm from centre of sphere of diameter 10 cm. Locate the image of bubble from (a) nearer surface and (b) farther surface.
View Solution
Knowledge Check
An air bubble in glass (μ = 1.5) is situated at a distance 3 cm from a convex surface of diameter 10 cm as shown. The distance from surface at which the image of bubble appears is
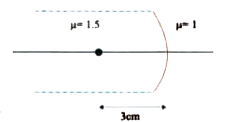 A2.5cmB5cmC4cmD1.5cm
A2.5cmB5cmC4cmD1.5cmA point object is situated in air at a distance of 20 cm from a convex refracting surface of 5cm radius. The position of the iamge is [μ=1.5]
A40 cmB30 cmC25 cmD15 cmThere is a small air bubble inside a glass sphere (μ=1.5) of radius 5 cm. The bubble is 7.5 cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10 cm below the surface of water. The bubble is viewed normally from air. Find the apparent depth on the bubble.
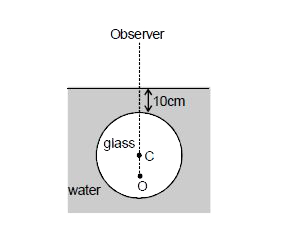 A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water
A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water
Fig shows a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. the bubble is 4.0 cm below the surface and is viewed normally from the outside. Find the apparent depth of the bubble.
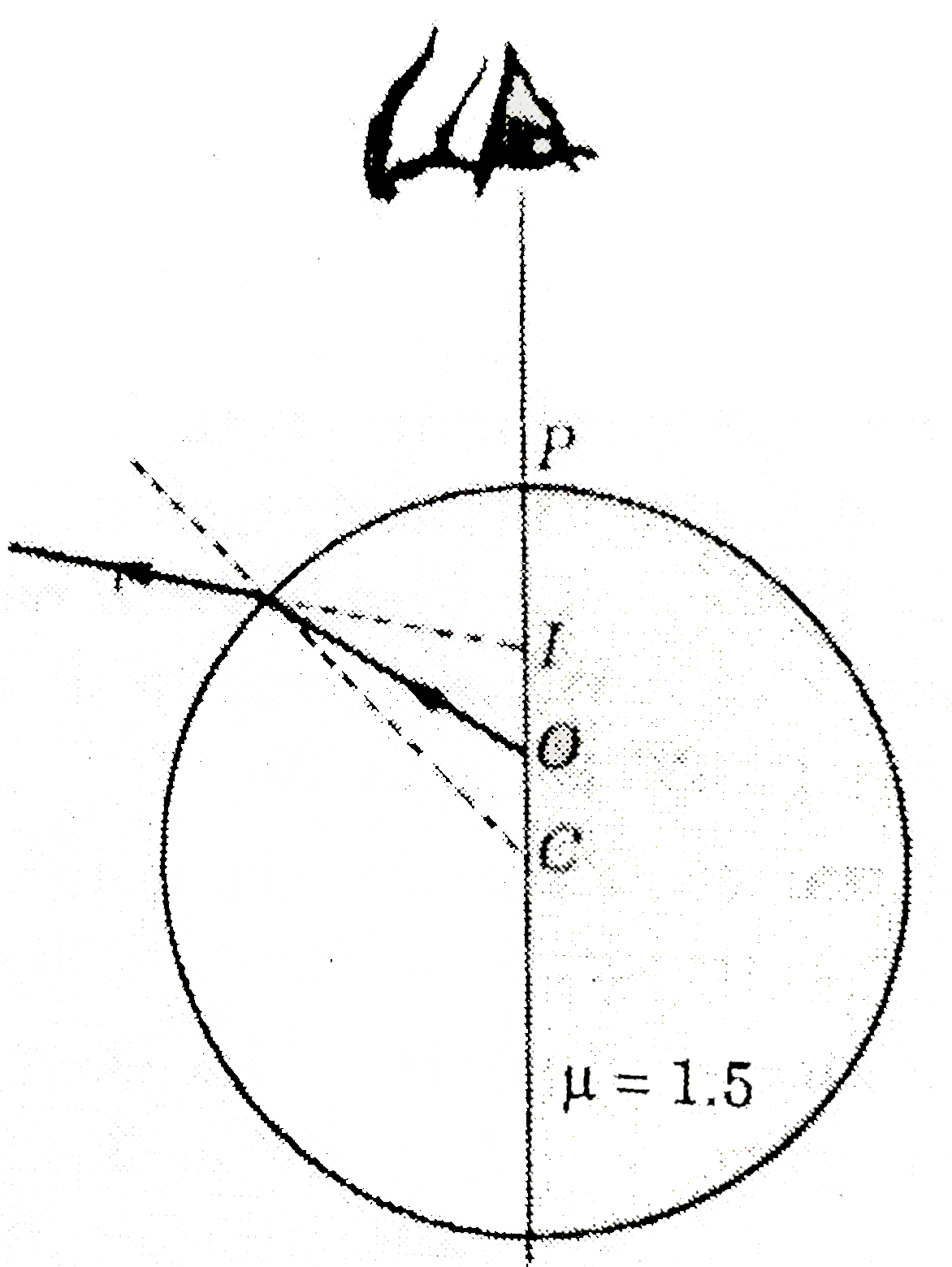
View SolutionAn air bubble is seen inside a solid sphere of glass (n=1.5) of 4.0cm diameter at a distance of 1.0cm from the surface of the sphere (on seeing along the diameter). Determine the real position of the bubble inside the sphere.
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA point mass is placed on the principal axis at 0 at a distance of 10cm from convex refracting surface of the pole.Find the image distance (in cms) from pole of refracting surface. (Radius of the spherical surface is R =30cm) n1=1.5
View SolutionAn air bubble inside a glass slab (µ=1.5) appears 6 cm when viewed from one side and 4 cm when viewed from the opposite side. The thickness of the slab is
View Solution

