A thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is

R2λ0
2πR2λ0
πR2λ02
πR2λ0
The correct Answer is:d
Dipole moment of the charge pair at P and Q
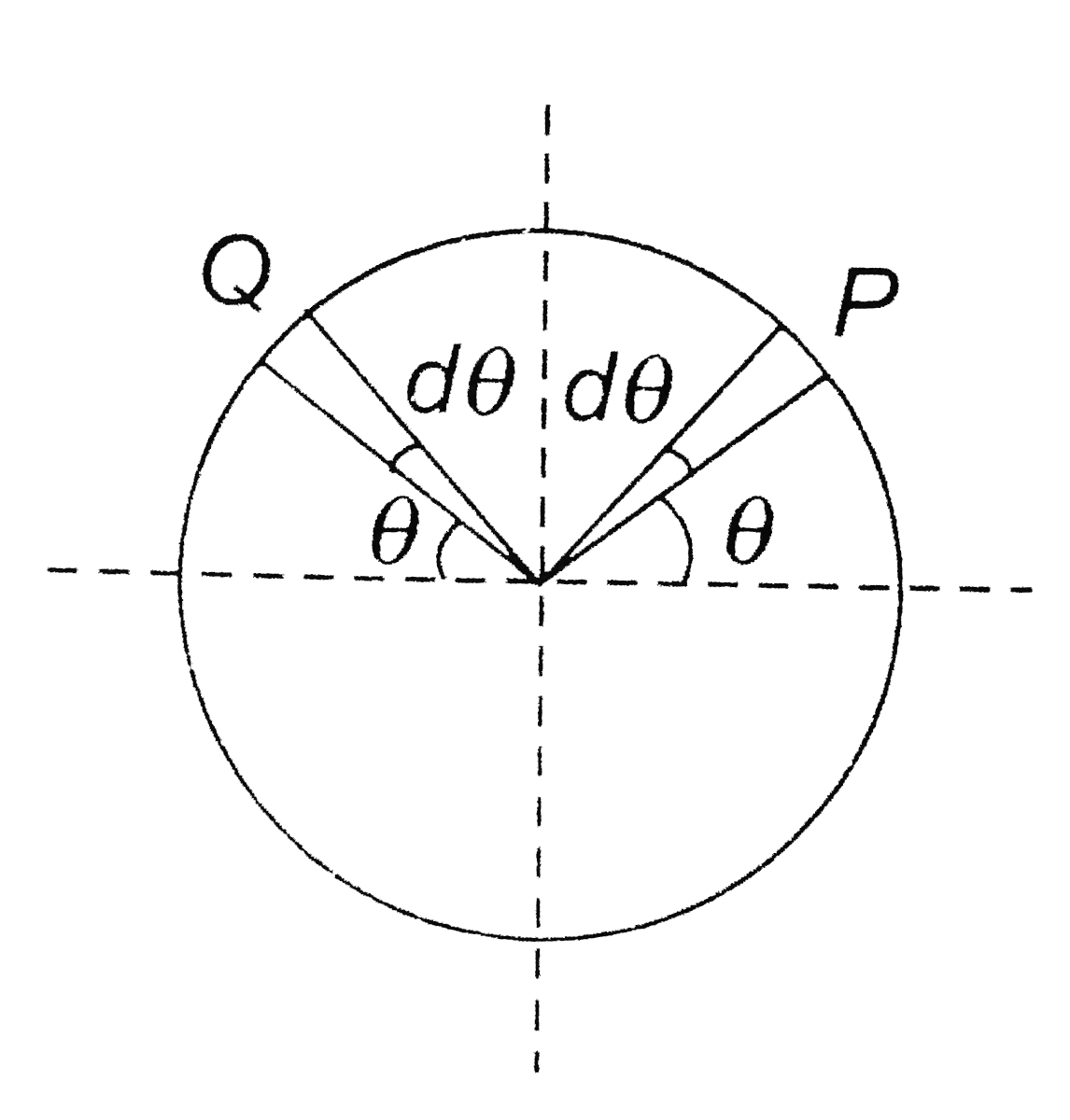
dp=[(λ0cosθ)Rdθ](2Rcosθ)
Total dipole moment
=2λ0R2π/2∫−π/2cos2θdθ=πR2λ0
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionA thin nonconducting ring of radius r has a linear charge density q=q0cosθ, where q0 is a constant and θ is the angle at the centre from the diameter of maximum charge density in the anticlockwise direction. Find the electric field at the centre of the ring.
View Solution
Knowledge Check
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2A non conducting ring of radius R1 is charged such that the linear charge density is λ1cos2θ where θ is the polar angle. If the radius is increased to R2 keeping the charge constant, the linear charge density is changed to λ2cos2θ. The relation connecting R1, R2λ1 and λ2 will be
Aλ1/R1=λ2/R2Bλ1/R2=λ2/R1Cλ1λ2=R1R2Dλ21R1=λ22R2Charge over a nonconducting ring is distributed so that the linear charge density varies as λ=λ0sinθ. What is the direction of force on a charge q0 placed at the center?
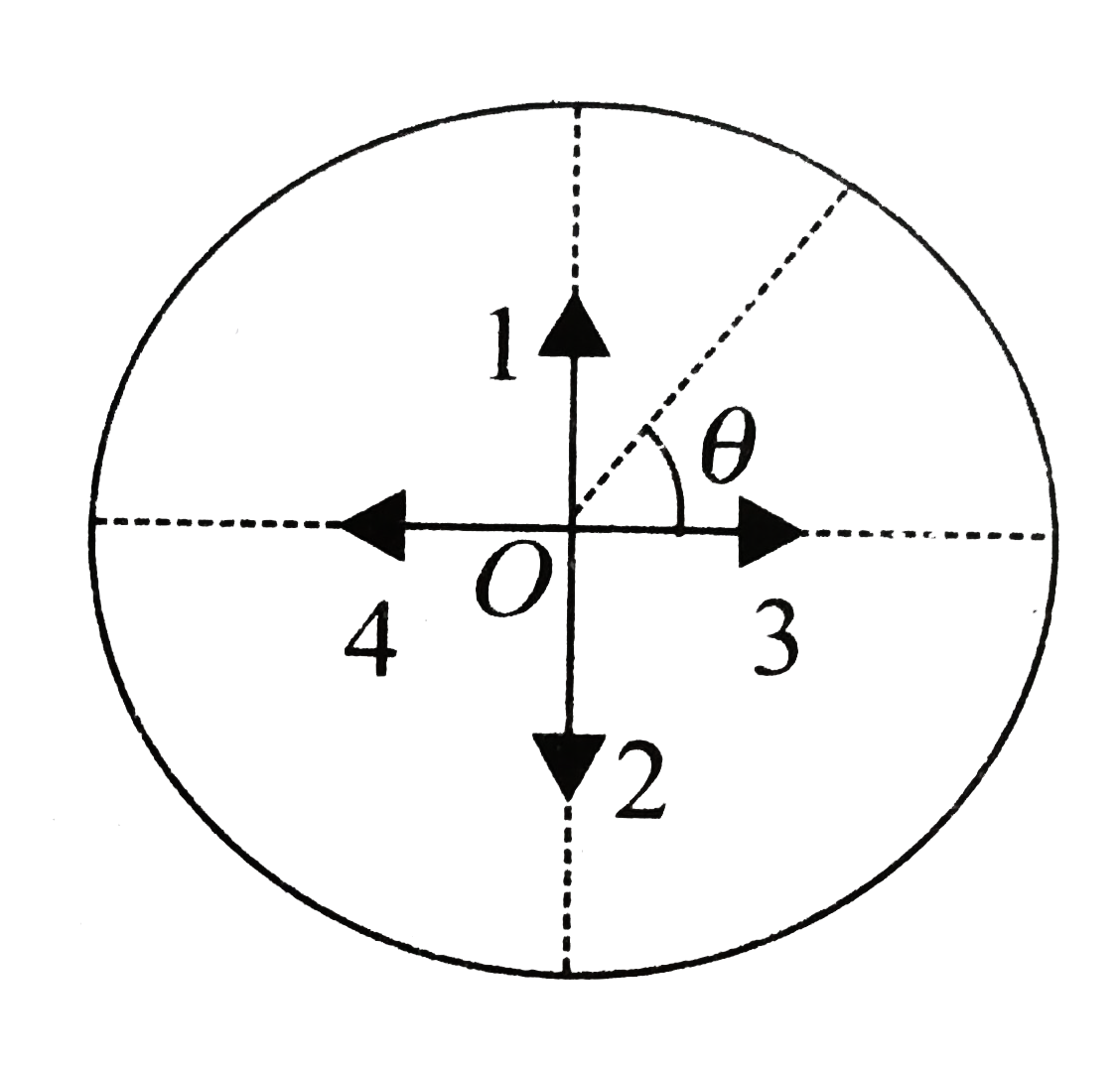 Aalong 1 if q0 is positive and 2 if q0 is negative.Balong 2 if q0 is positive and 1 if q0 is negative.Calong 3 if q0 is positive and 4 if q0 is negative.Dalong 4 if q0 is positive and 3 if q0 is negative.
Aalong 1 if q0 is positive and 2 if q0 is negative.Balong 2 if q0 is positive and 1 if q0 is negative.Calong 3 if q0 is positive and 4 if q0 is negative.Dalong 4 if q0 is positive and 3 if q0 is negative.
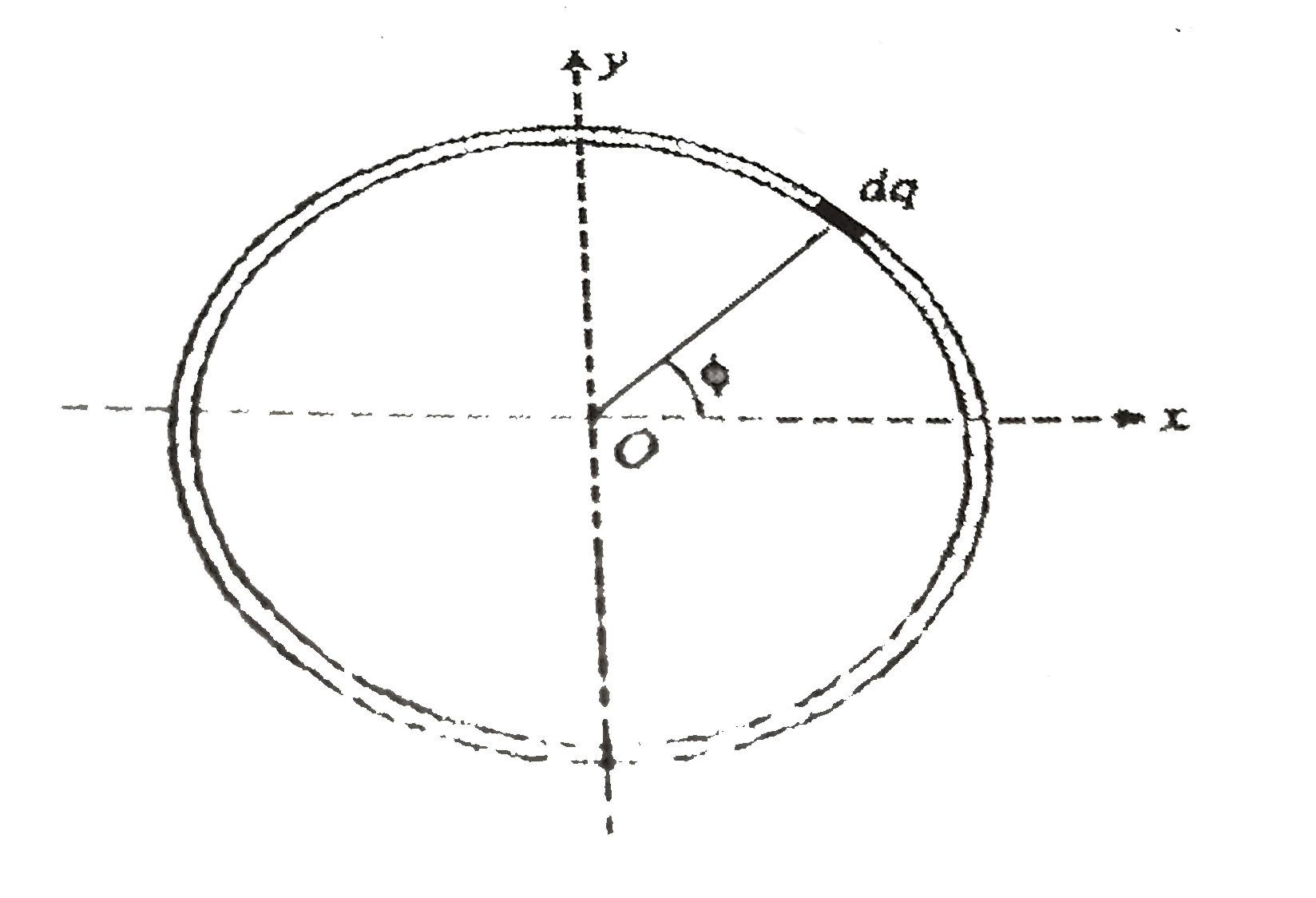
A thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :
View SolutionA non conducting ring of radius R is charged as shown in figure : Figure

View SolutionA circular wire of radius r has a uniform linear charge density λ=λ0cos2θ, The total charge on the wire is απλ0r2 Find α.
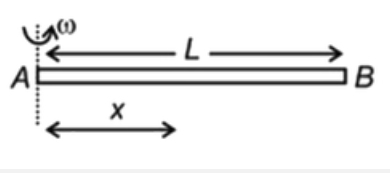
View SolutionA non - conducting rod of length L with linear charge density λ=λ0x where x is the distance from end A is rotating with constant angular speed ω about the same end. If the angular velocity of the rod (ω) is large, then the magnetic dipole moment of the system is ωλ0L4n. What is the value of n?
View SolutionA rod with linear charge density λ is bent in the shap of circular ring. The electric potential at the centre of the circular ring is
View Solution