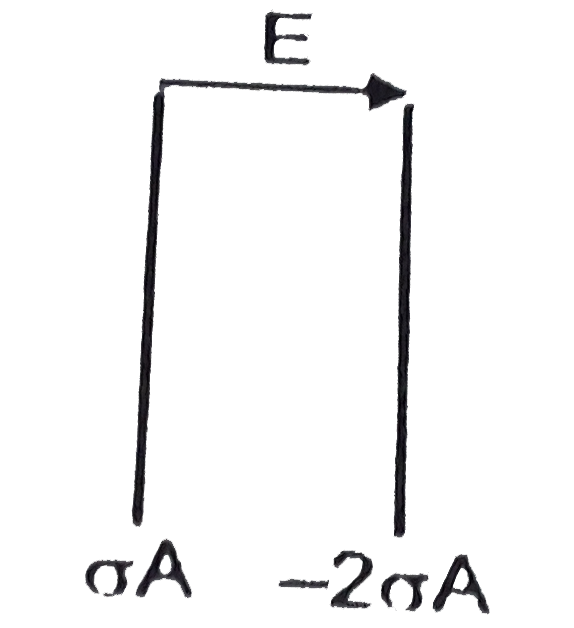
An uncharged conducting large plate is placed as shown. Now an electric field E towards right is applied. Find the induced charge density on the right surface of the plate.

−ε0E
ε0E
−2ε0E
2ε0E
The correct Answer is:B
Net electric field at point P should be zero. For the electric field due to induced charges= applied electric field

⇒σε0=E⇒σ=ε0E
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section B - Assertion Reasoning
Explore 25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:AIPMTNEET Questions
Explore 24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Dipole
Explore 29 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Find the electric field at the center of the sphere due to the induced charges on the surface of the sphere, as shown in Fig. 22-30.

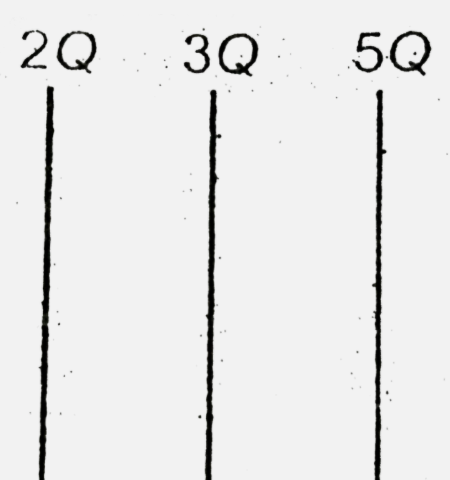
View SolutionThree charged conducting plates are separated by small distances as shown in figure. The charges on the plates are shown. Find the ratio of charge on right surface and left surface of the middle plate.
View Solution
Knowledge Check
A charge q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre and just above the surface of the plate is 50 V/m. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same uniform charge q, the electric field at the point P will become :
AzeroB25 V/mC50 V/mD100 V/mAn electron is projected from a distance d and with initial velocity u parallel to a uniformly charged flat conducting plate as shown. It strikes the plate after travelling a distance l along the direction of projection. The surface charge density of the conducting plate is equal to
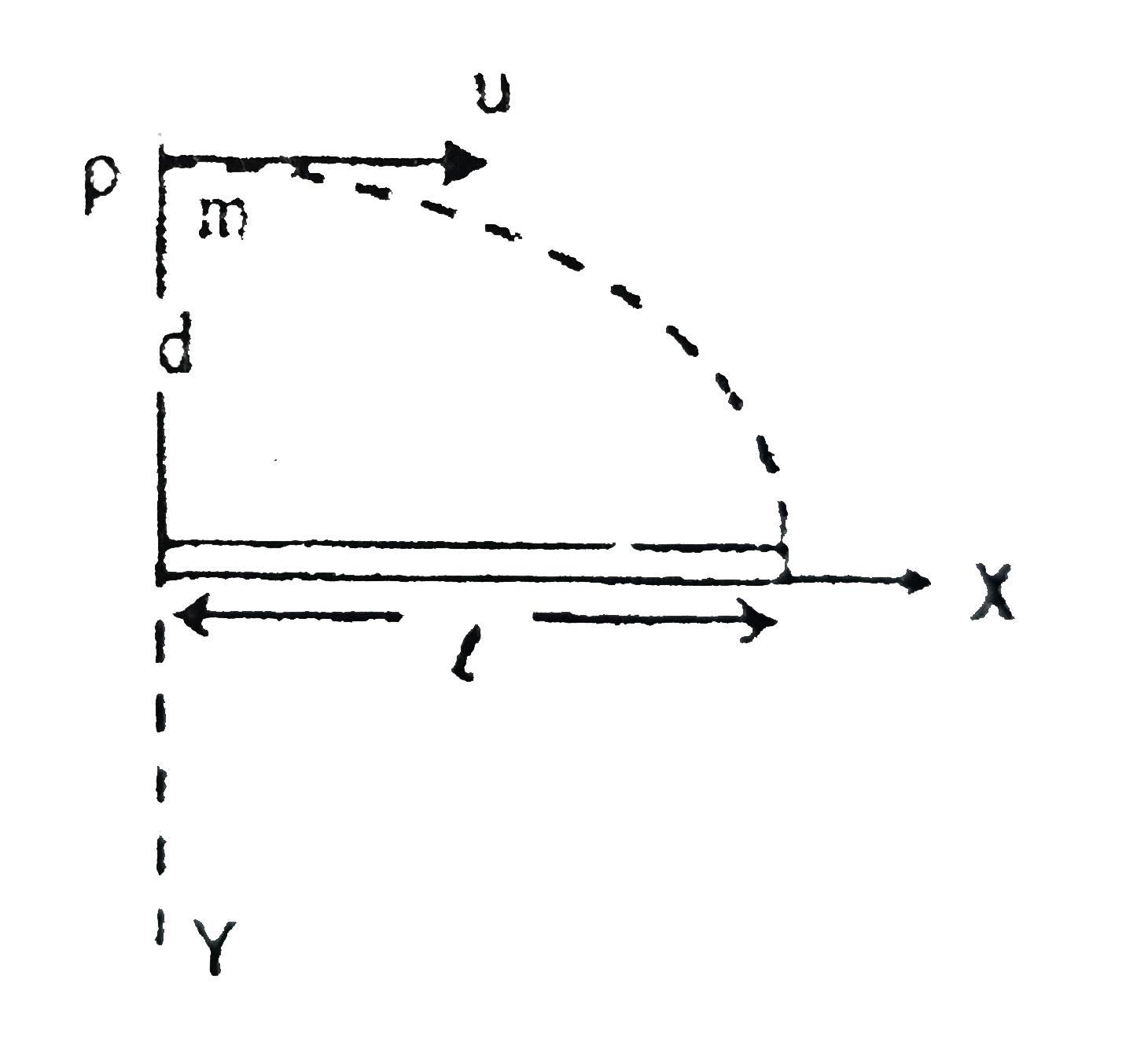 A2dε0mu2el2B2dε0muelCdε0mu2elDdε0muel
A2dε0mu2el2B2dε0muelCdε0mu2elDdε0muelTwo large plates are given the charges as shown in figure. Now, the left plane is earthed. Find the amount of charge that will flow from the earth to the plate.
 A14μCB−14μCC7μCD−7μC
A14μCB−14μCC7μCD−7μC
Two conducting plates X and Y, having large surface area A (on one side), are placed parallel to each other as shown in figure. The plate X is given a charge Q whereas the other is neutral. Find :
(a) The surface charge density at the inner surface of the plate X,
(b) The electric field at a point to the left of the plates,
(c) The electric field at a point in between the plates and
(d) The electric field at a point to the right of the plates.
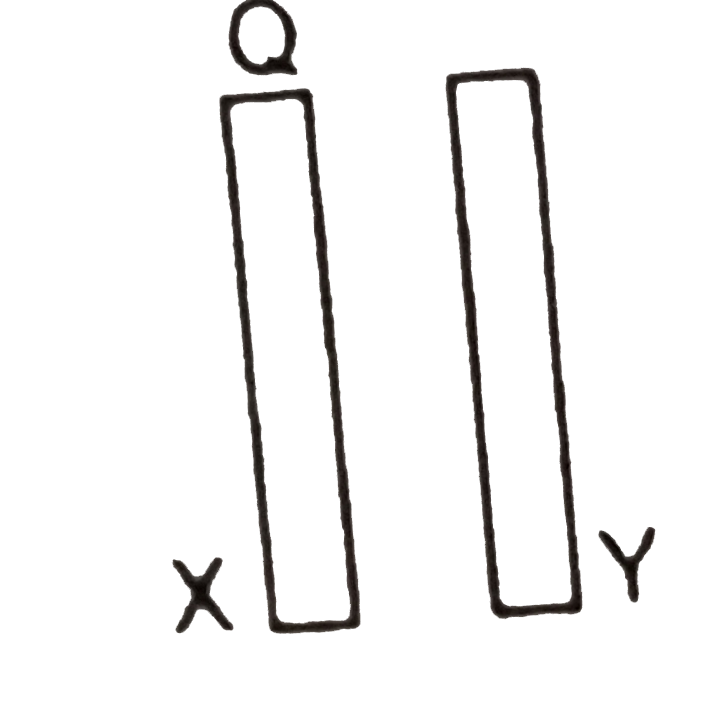
View SolutionTwo thin conducting plates (very large) parallel to each other carrying total chares σA and −2σ A respectively (where A is the area of each plates), are placed in a uniform external electric field E as shown. Find the surface charge on each surface.
View SolutionWhen an uncharged conducting ball of radius R is placed in an external uniform electric field, a surface charge densityh σ=σ0cosθ is induced on the ball's surface charge (here σ0 is a constant, θ is a polar angle). Find the magnitude of the resultant electric force acting on an induced charge of the same sign.
View SolutionTwo large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X ia given a charge Q whereas the other is neutral. Find (a) the surface charge dendity at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.

View SolutionA solid conducting sphere of radius R is placed in a uniform electric field E as showo in figure. Due to electric field non uniform surface charges are induced on the surface of the sphere. Consider a point A on the surface of sphere at a polar angle θ from the direction of electric field as shown in figure. Find the surface density of induced charges at point A in terms of electric field and polar angle θ : lt brgt

View Solution