A charge q is placed at the some distance along the axis of a uniformly charged disc of surface charge density σ. The flux due to the charge q through the disc is ϕ. The electric force on charge q exerted by the disc is
σϕ
σϕ4π
σϕ2π
σϕ3π
The correct Answer is:a
To find the electric force on charge q exerted by the uniformly charged disc with surface charge density σ, we can follow these steps:
Step 1: Understand the Problem
We have a charge q placed at a distance from a uniformly charged disc with surface charge density σ. The electric flux ϕ through the disc due to the charge q is given.
Step 2: Relate Electric Flux to Charge
The electric flux ϕ through the disc due to the charge q can be expressed using Gauss's Law:
ϕ=q2ϵ0(1−cosθ)
where θ is the half-angle subtended by the disc at the charge q.
Step 3: Find the Electric Field Due to the Disc
The electric field E at a distance x from the center of the disc can be derived from the surface charge density σ:
E=σ2ϵ0(1−x√x2+R2)
where R is the radius of the disc and x is the distance from the disc to the charge q.
Step 4: Calculate the Electric Force on Charge q
The electric force F on the charge q due to the electric field E from the disc is given by:
F=qE
Substituting the expression for E:
F=q⋅σ2ϵ0(1−x√x2+R2)
Step 5: Simplify the Expression
Now, we can simplify the expression for the electric force:
F=qσ2ϵ0(1−x√x2+R2)
Final Result
Thus, the electric force on charge q exerted by the disc is:
F=qσ2ϵ0(1−x√x2+R2)
We have a charge q placed at a distance from a uniformly charged disc with surface charge density σ. The electric flux ϕ through the disc due to the charge q is given.
The electric flux ϕ through the disc due to the charge q can be expressed using Gauss's Law:
ϕ=q2ϵ0(1−cosθ)
where θ is the half-angle subtended by the disc at the charge q.
The electric field E at a distance x from the center of the disc can be derived from the surface charge density σ:
E=σ2ϵ0(1−x√x2+R2)
where R is the radius of the disc and x is the distance from the disc to the charge q.
The electric force F on the charge q due to the electric field E from the disc is given by:
F=qE
Substituting the expression for E:
F=q⋅σ2ϵ0(1−x√x2+R2)
Now, we can simplify the expression for the electric force:
F=qσ2ϵ0(1−x√x2+R2)
Thus, the electric force on charge q exerted by the disc is:
F=qσ2ϵ0(1−x√x2+R2)
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
A point charge placed on the axis of a uniformly charged disc experiences a force f due to the disc. If the charge density on the disc sigam is, the electric flux through the disc, due to the point charge will be
A2πfσBf2πσCf2σDfσA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
AQ/4ε0BQ/4πε0CQ/2ε0DQ/2πε0
A point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
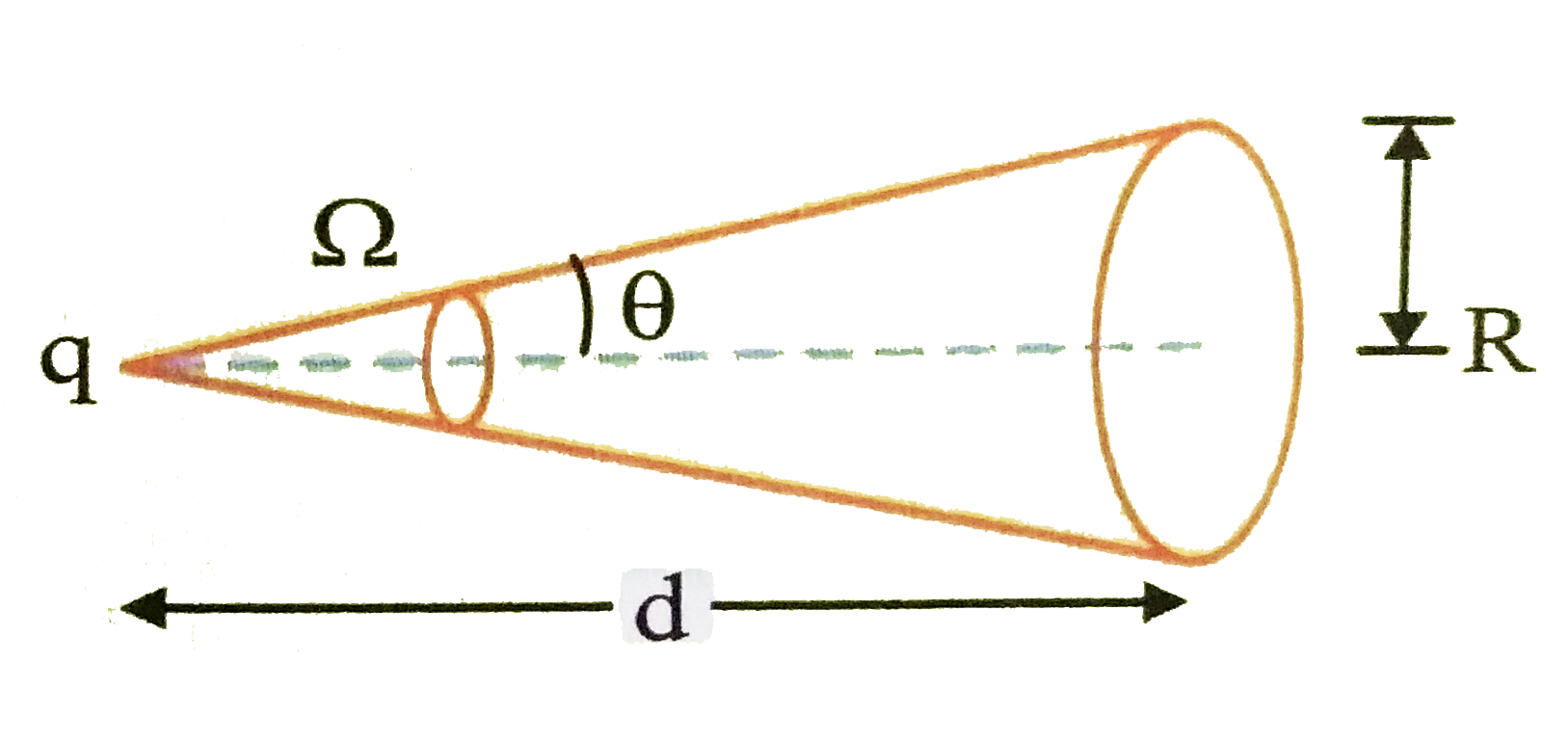
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionA charge q is placed at the centre of an imaginary spherical surface. What will be the electric flux due to this charge through any half of the sphere.
View SolutionFind the electric potential at the axis of a uniformly charged disc and use potential to find the electric field at same point.
View SolutionCalculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density σ and R which also contains a concentric hole of radius r.
View SolutionThe diagram shows a part of disc of radius R carrying uniformly distributed charge of density σ. Electric potential at the centre O of parent disc is
View Solution