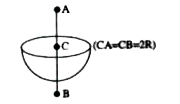
Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

ρR/6ε0+E
ρR/12ε0−E
−ρR/6ε0+E
ρR/12ε0+E
The correct Answer is:B
Let us complete the sphere. Electric field due lower part at A= electric field due to upper part
B=E (given)
Electric field due to lower part at B= electric field due to full sphere- electric field due to upper part
KQ(2R)2−E=14πε0ρ(4/3)πR34R2−E=ρR12ε0−E

Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section B - Assertion Reasoning
Explore 25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:AIPMTNEET Questions
Explore 24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Dipole
Explore 29 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Assertion: Electric lines of force cross each other
Reason: Electric field at a point superimpose to give one resulant electric field
View SolutionA simple pendulum of period T has a metal bob which is negatively charged. If it is allowed to oscillate above a positively charged metal plate, its period will
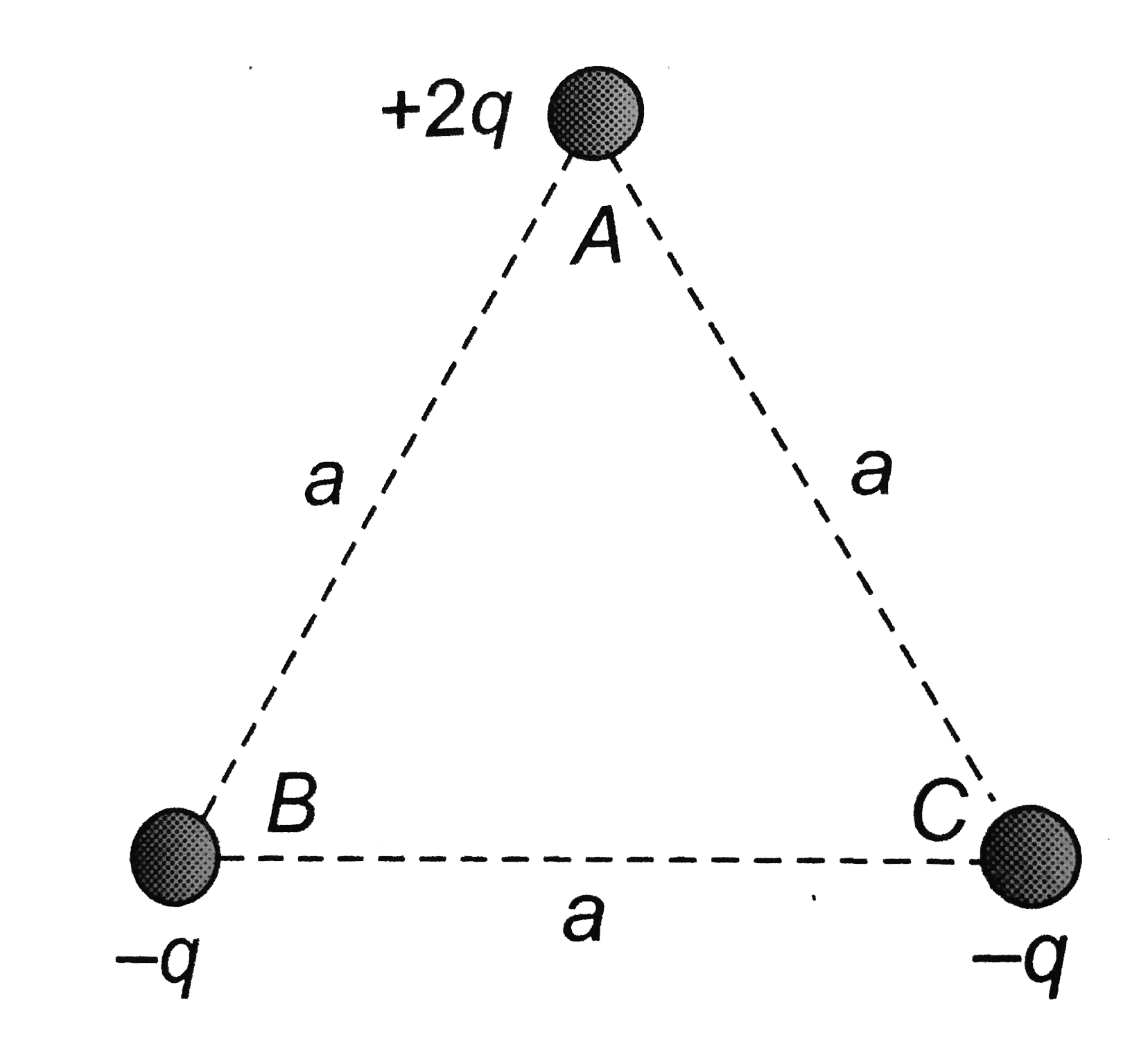
View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
View SolutionIf a photon has velocity c and frequency n , then which of following represents its wavelength ?
View SolutionGiven: electric potential, ϕ=x2+y2+z2. The modulus of electric field at (x,y,z) is
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density rho . If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance ( R )/(2) from the centre will be
View SolutionR त्रिज्या का एक अचालक ठोस गोला एकसमान रूप से आवेशित किया गया है। गोले के कारण इसके केन्द्र से r दूरी पर वैद्युत क्षेत्र का परिमाण है
View SolutionR त्रिज्या की एकसमान आवेशित चकती के केंद्र से कितनी दूरी पर विद्युत क्षेत्र का मान केंद्र पर विद्युत क्षेत्र का मान का आधा होगा?
View Solutionयदि पृथक्कृत कुचालक गोले की त्रिज्या R तथा आवेश घनत्व (ρ) है। गोले के केन्द्र से r दूरी (r<R) पर वैद्युत क्षेत्र होगा
View SolutionA hemispherical shell is uniformly charge positively. The electric field at point on a diameter away from the center is directed
View SolutionThe diagram shows a uniformly charged bemisphere of radius R. It has volume charge density ρ. If the electric field at a point 2R distance below its centre ?
View SolutionR is the total charge + Q on a sphere of radius which is uniformly distributed throughout its volume. At a 2R distance from the center of the sphere, a particle of + q charge is a constant inertia. A point P lies on the surface of the sphere and the line connecting the center of the sphere and the point charge. For what value of q will the electric field at P be zero -
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density rho . If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
View Solutionएक बिंदु आवेश q को आंतरिक त्रिज्या 2R और बाहरी त्रिज्या 3R के एक चालक कोश के केंद्र से R की दूरी पर रखा जाता है। कोश के केंद्र पर विधुत विभव होगा :
View Solution