Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

ρR/6ε0+E
ρR/12ε0−E
−ρR/6ε0+E
ρR/12ε0+E
The correct Answer is:B
b. Let us complete the sphere. Electric field due to lower part at
A is equal to electric field due to upper part at B = E (given)
Electric field due to lower
part at B = electric field due
to full sphere - electric field
due to upper part
=kQ(2R)2−E
=14πε0ρ(4/3)πR34R2−E
=ρR12ε0−E

Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Comprehension
Explore 36 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
There is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution(a) Use Gauss's law to show that due to a uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R. (b) Two point charges of +1μC and +4μC are kept 30 cm apart. How far from the +1μC charge on the line joining the two charges, will the net electric field be zero ?
View Solution
Knowledge Check
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2An insulated sphere of radius R has a uniform volume charge density λ. The electric field at a point A, which is at distance r from its center is given by (R>r)
AZeroBRλ/3∈0C2rλ3∈0Drλ3∈0An insulated sphere of radius r haas a uniform volume charge density λ. The electric field at a point A, which is at distance r from its centre is given by (R>r)
AZeroBRλ/3∈0C2rλ3∈0Drλ3∈0
The diagram shows a part of uniformly charged disc of radius R having surface charge densityo. If electric potential at the center O is Then find N. 1 N Х OR 280 R R/2
View SolutionUse Gauss's law to show that due to uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionA spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
View SolutionFigure shows a uniformly charges hemispherical shell. The direction of electric field at point p that is off centre (but in the plane of the largest circle of the hemisphere), will be along
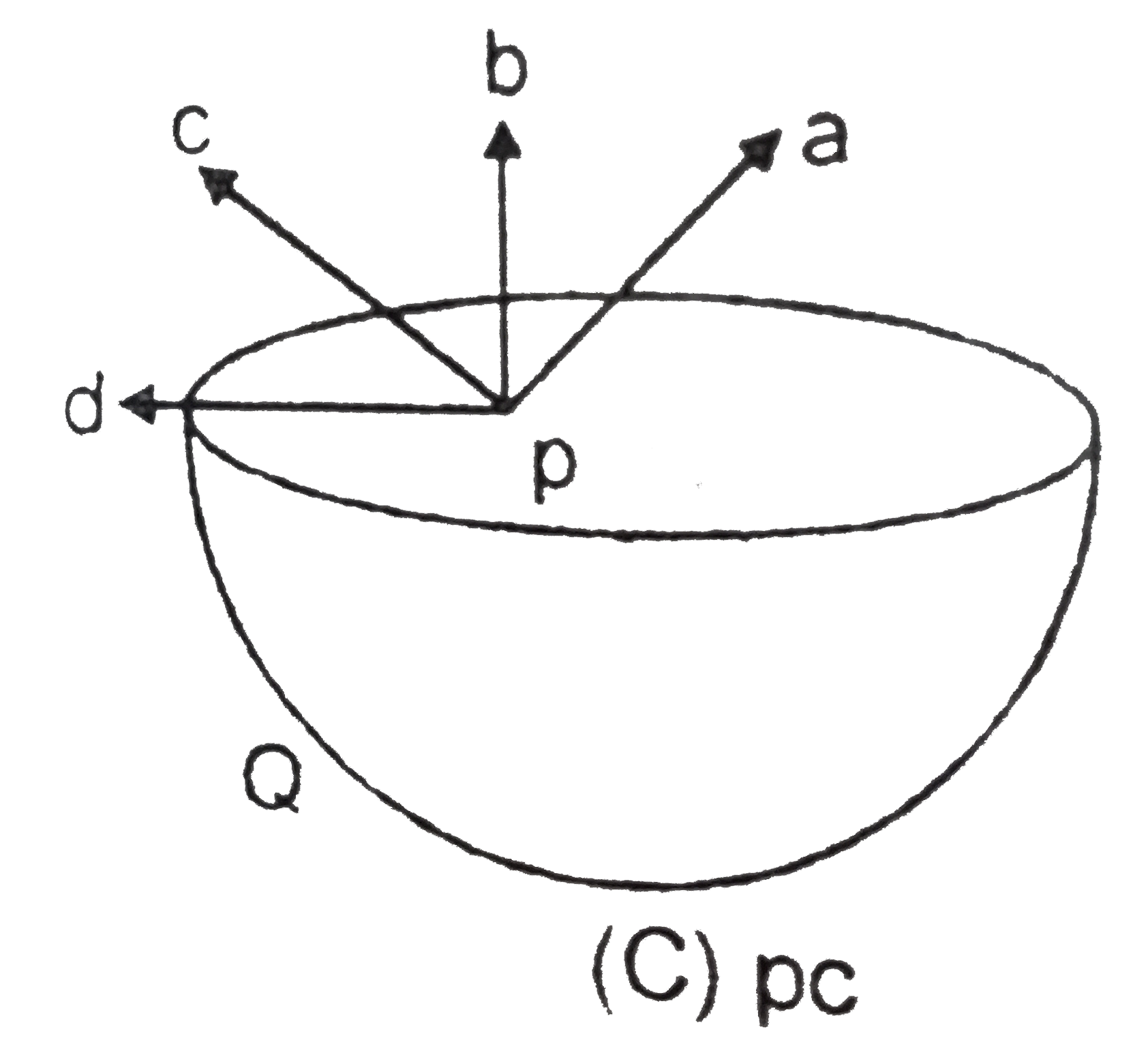
View Solution

