Figure shows a uniformly charges hemispherical shell. The direction of electric field at point that is off centre (but in the plane of the largest circle of the hemisphere), will be along
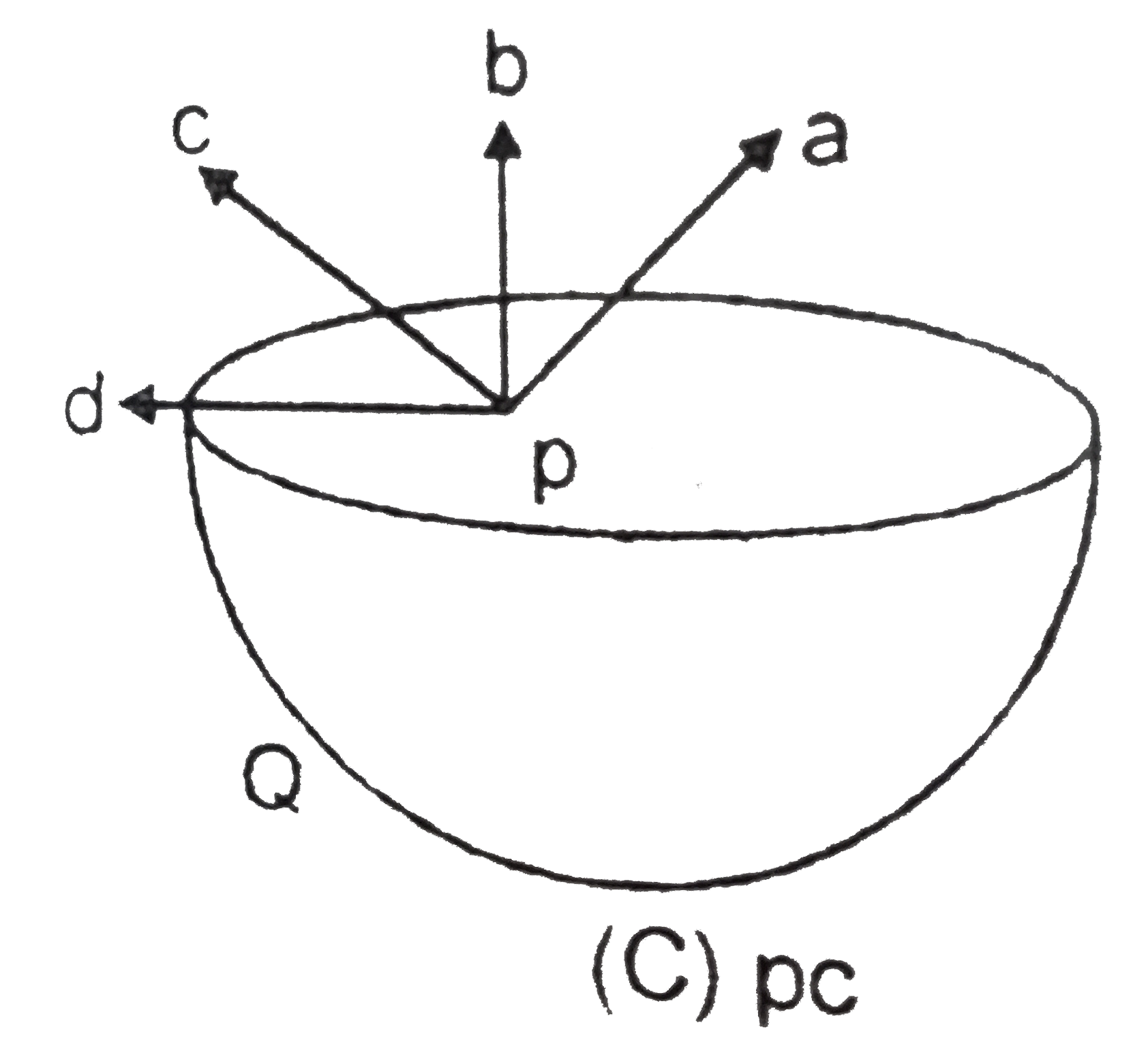
The correct Answer is:B
Let electric field at pt 'p' has both 'x' and y component
So similar electric field will be for other hemisphere (upper half)
Now lets overlap both

and it should be zero (as E inside a full shell = 0)
So , so electric field at 'p' is purely in y direction
 .
.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.33
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.30
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
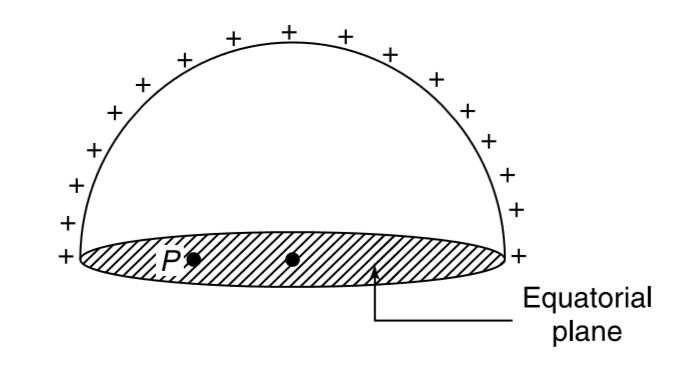
Consider a uniformly charged hemispherical shell. What can you say about the direction of electric field at points on the equatorial plane. (e.g. point P)
View SolutionUse Gauss's law to show that due to uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R.
View Solution
Knowledge Check
Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
 AρR/6ε0+EBρR/12ε0−EC−ρR/6ε0+EDρR/12ε0+E
AρR/6ε0+EBρR/12ε0−EC−ρR/6ε0+EDρR/12ε0+EFigure show a hemispherical shell having uniform mass density The direction of gravitational field at point P will be along
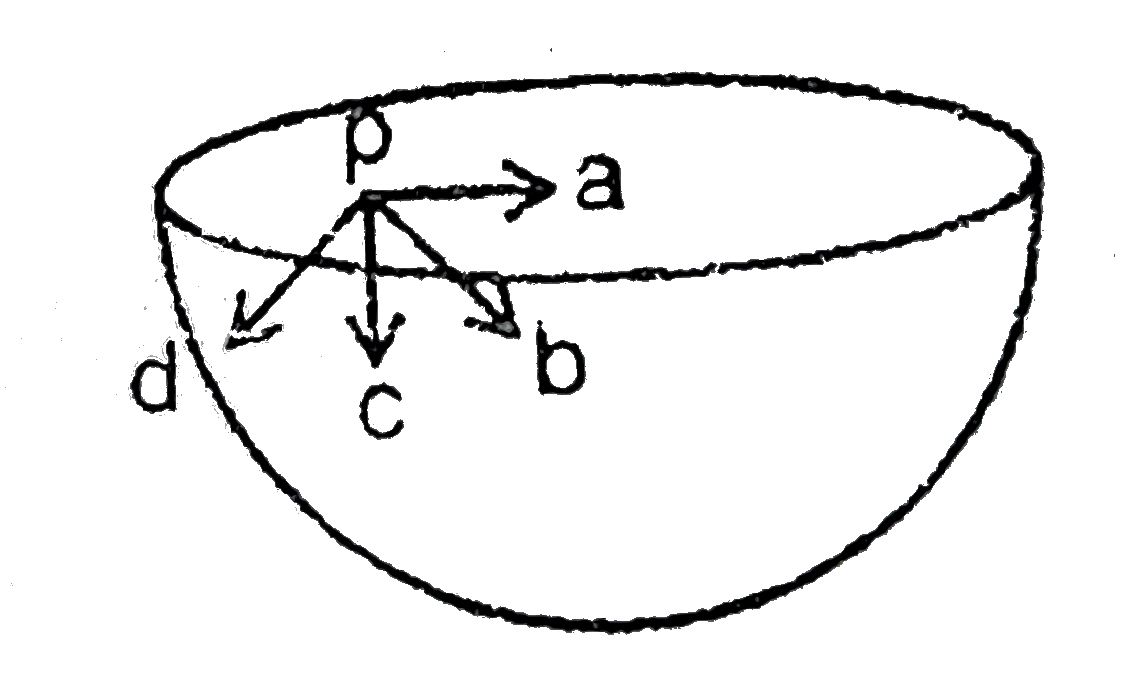 .AaBbCcDd
.AaBbCcDdA hemispherical shell is uniformly charge positively .the electric field at point on a diameter away from the centre is directed
Aperpendicular to the diameterBparallel to the diameterCat an angle titled towards the diameter.Dat an angle tilted away from thke diameter.
(a) Use Gauss's law to show that due to a uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R. (b) Two point charges of +1μC and +4μC are kept 30 cm apart. How far from the +1μC charge on the line joining the two charges, will the net electric field be zero ?
View SolutionUsing Gauss's theorem show mathematically that for any point outside the shell , the field due to a uniformaly charged thin spherical shell is the same as if the entire charge of the shell is concentrated at the centre? Why do you expect the electric field inside the shell to be zero according to this theorem?
View SolutionA hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed.
View SolutionA hemispherical shall is uniformly charge positively .the electric field at point on a diameter away from the centre is directed
View SolutionA uniformly charged non-conducting spherical shell is given +q charge and a point charge -q is placed as shown. The electric field lines will be

View Solution

